Zeichung und Berechnung?
Aufgabe: Eine Badewanne wird in 10 Minuten mit 200 Liter Wasser gefüllt. Nach einer halben Stunde Badezeit läuft das Wasser in 6 Minuten wieder ab.
a) Zeichne einen Graphen zur Wassermenge (in Liter) in der Badewanne im Zeitraum von 50 Minuten. (Beschrifte die Achsen sinnvoll.)
b) Berechne die Änderung der Wassermenge in l/min beim Zulauf, beim Baden und beim Abfließen des Wassers.
Nun weiß ich wirklich nicht wie ich vorgehen muss.
in 10 Minuten ist die Badewanne mit 200 Liter Wasser gefüllt
nach 30 Minuten Badezeit läuft das Wasser in 6 Minuten ab
x-Achse = Zeit
y-Achse = ??? Wasser Liter ????
Wie lautet die Formel ???
Ich war krank und habe vieles verpasst bitte hilft mir ....
Dankeschön im Voraus
3 Antworten
a)
So sieht der Graph aus. Von 46 min bis 50 min müsste man noch eine Gerade auf der x-Achse zeichnen.
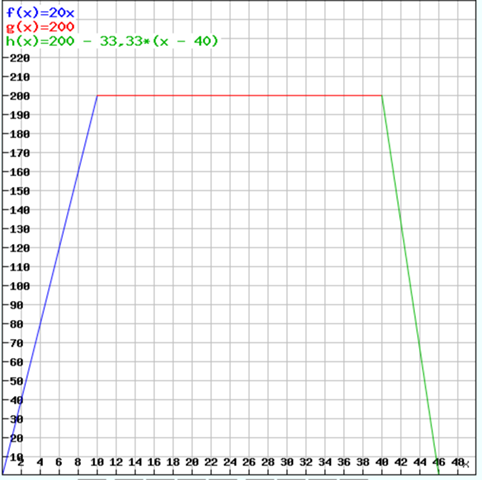
Beschriftung x-Achse: t in min
Beschriftung y-Achse: V in l
b) Hier geht es nicht um die Füllmenge der Badewannde wie im Graphen, sondern es geht um die Änderung des Volumens V'.
Dazu müssen wir die Änderung Füllmenge durch die Zeit dividieren, die für diese Änderung erforderlich ist:
Intervall 1 von 0 bis 10 min:
ΔV = 200 l
Δt = 10 min
V' = ΔV / Δt = 200 l / 10 min = 20 l/min
Intervall 2 von 10 min bis 40 min:
ΔV = 0 l
Δt = 30 min
V' = ΔV / Δt = 0 l / 30 min = 0 l/min
Intervall 3 von 10 min bis 40 min:
ΔV = 200 l
Δt = 6 min
V' = ΔV / Δt = 200 l / 6 min = 33,33 l/min
Sehr hilfreich. Ich wusste wirklich nicht weiter....... vielen vielen Dank
x-Achse = Zeit
y-Achse = Menge an Wasser in Der Wanne zum Zeitpunkt der auf der x-Achse steht
Du brauchst erstmal gar keine Formel, nur die Zeichnung.
Die ersten 10 Minuten steigt der graph an bis zu einer Höhe von 200l.
Dann bleibt der graph bis zur Minute 40 parallel.
Dann fällt er bis auf Null bis zur Minute 46.
Die letzten 4 Minuten bis 50 Minuten bleibt er dann auf Null.