Wie skizziere ich diese Teilmenge?
Hallo zusammen,
Ich tue mich immer noch schwer mit dem skizzieren von Teilmengen. Als letzter Teil einer Aufgabe soll ich die Teilmenge M = {f(x,y) | |x| ≤ 1, |y| ≤ 1} skizzieren und bestimmen, ob sie zusammenhängend sind.
Ich habe zwar so eine Idee, bin aber bei dem ganzen Thema sehr unsicher und um jede Hilfe dankbar!
Schöne Feiertage euch allen!
3 Antworten
Hallo,
so, jetzt nochmal, aber mit der Funktion f.
Bedingung (1) : |x|+|y| < 1
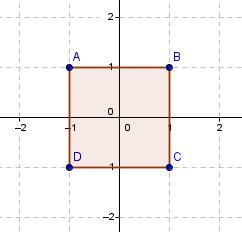
Die Menge der Punkte P(x,y) in der xy-Ebene, die die Bedingung (1) erfüllen, liegen in einem Quadrat mit den Eckpunkten A(-1;0), B(0;1), C(1;0), D(0;-1).
Alle Punkte, deren Koordinaten innerhalb des blauen Quadrats liegen, erfüllen die Bedingung (1). Die Koordinaten der Punkte A,B,C,D und der Segmente [AB], [BC], [CD], [DA] erfüllen die Bedingung |x|+|y| = 1, d.h. sie bilden den Rand des blauen Quadrats.
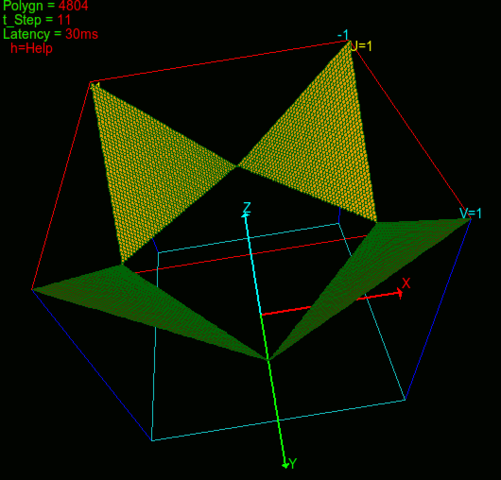
Die Punkte der Menge M, deren xy-Koordinaten die Bedingung (1) erfüllen, besitzen die z-Koordinate 2. Sie bilden also ein Quadrat wie das auf dem Bild in der xy-Ebene, in der Höhe 2. ( M(x;y;2) ).
Dieser Teil der Menge M ist also ein in der z-Höhe 2 "schwebendes" Quadrat ohne Rand und ohne die Eckpunkte.
Nun kommt der zweite Teil der Menge M, die der
Bedingung (2) : "sonst"
genügt. Was bedeutet das? Das sind alle Punkte M(x;y;z), für deren xy-Koordinaten nicht |x|+|y| < 1 gilt. Für sie gilt also |x|+|y| ≥ 1. Dabei dürfen wir nicht vergessen, dass sie zusätzlich die Bedingung (0): |x| ≤ 1und |y| ≤ 1 erfüllen müssen.
Alle Punkte P(x;y) der xy-Ebene, deren Koordinaten der Bed. (0) genügen, sind die Punkte des Quadrates E(-1;1), F(1;1), G(1;-1), H(-1;-1) samt des Randes des Quadrats.
Die Punkte P(x;y), die der Bedingung (0) und der Bedingung (2) genügen, sind alle Punkte P, die im roten, aber nicht im blauen Quadrat liegen. Sie dürfen aber auf dem Rand des blauen Quadrates liegen.
Die Punkte M(x;y;z), deren xy-Koordinaten die Bedingungen (0) und (2) erfüllen (also "sonst"), erreichen an den Eckpunkten des roten Quadrates die Höhe 2. Ansonsten liegen sie darunter. Je mehr sich M(x;y;z) in der xy-Ebene dem Ursprung des Koordinatensystems nähert, umso geringer ist die Höhe z. M kann sich unter den Bedingungen (0) und (2) aber nur bis zum Rand des blauen Quadrats nähern, wo M die Höhe 1 hat.
Das zweite BIld zeigt die Punkte M unter den Bedingungen (0) und (2). Es sind vier Dreiecke, deren Spitze die Punkte E'(-1;1;2), F'(1;1;2), G'(1;-1;2) und H'(-1;-1;2) sind.
Wir haben also folgende Situation:
Über dem Blauen Quadrat "schwebt" dasselbe Quadrat in der z-Höhe 2. Das sind Punke von M. (Bedingung 1). Dieses Quadrat ist ohne Rand.
Sowie M auf dem xy-Rand des offenen Quadrates ABCD liegt, springt M auf die Höhe 1.
Die Menge M ist die Vereinigung der Mengen M1 und M2, wobei die Koordinaten von M1 der Bedingung 1 und die der Menge M2 den Bedingungen 0 und 2 genügen: M = M1 ∪ M2. Dabei ist M1 offen und M2 abgeschlossen, M ist also nicht die Vereinigung zweier offener disjunkter Mengen, also müsste M zusammenhängend sein.
Ich hoffe Du konntest folgen. Ich bitte zu Bedenken, dass ich mich irren kann, also denke auch selber darüber nach.
Grüsse!

Ich korrigiere mein Argument zum Zusammenhang.
M ist ja eine Teilmenge von ℝ³, M die Vereinigung von M1 und M2.
Im ℝ³ kann man M1 und M2 jeweils in einen offenen 3-dimensionalen ε-Schlauch packen, sagen wir M1 ⊂ M1_ε und M2 ⊂ M2_ε.
M1_ε und M2_ε sind offene Mengen des R^3 und disjunkt, also ist M nicht zusammenhängend.
Hallo,
Ich sehe gerade, dass in der Definition der Menge M nicht (x;y), sondern f(x;y) steht. (Das f hatte mein Gehirn ausgeblendet...).
Ohne die Funktion f zu kennen kann die Frage nicht beantwortet werden. Die Information müsstest Du noch bringen.
Die Koordinaten (x;y) selbst beschreiben das Innere des Quadrats samt Rand. (Siehe Bild).
Grüsse
Oh danke, dass habe ich ganz vergessen! Die Funktion ist f(x,y) = 2 falls |x| + |y| < 1 und sonst = |x| + |y|. Vielen Dank für deine Hilfe!
Hallo!
|x|<=1 bedeutet, dass x im Intervall [-1; 1] liegt.
Für y ebenso.
Welche Fläche erhält man, wenn beide Koordinaten zwischen -1 und 1 variieren?
(Angenommen dass x und y in den reellen Zahlen variieren; das müsste eigentlich in der Definition von M noch dabei stehen))
Grüsse
Noch zwei Hinweise:
Zeichne die vier Geraden x=1, x= -1, y= 1, y= -1.
Der Punkt M(x;y) mit den Koordinaten (x;y) kann nicht "höher als 1", nicht "tiefer als -1", nicht "mehr rechts als 1", nicht "mehr links als -1" sein.