Wie schaffe ich es dieses Quadrat in dieses Drachenviereck rein zu konstruieren?

Foto:

Answer 1

[ralphdieter]

Idee: Das kleine Dreieck über dem Quadrat ist ähnlich zum halben Drachen.

So könnte es klappen:

1. Konstruiere ein (großes) Quadrat mit der waagrechten Drachen-Diagonale als obere Seite.
2. Verbinde den linken und rechten Seitenmittelpunkt dieses Quadrats mit der oberen Ecke des Drachens.
3. Die Verbindungslinien schneiden die waagrechte Diagonale in P und Q.
4. Zeichne die Senkrechten durch P und Q. Das sind zwei Seiten des gesuchten Quadrats.

Dass das so konstruierte Rechteck tatsächlich ein Quadrat ist, müsste man mit dem Strahlensatz zeigen können.

Answer 2

[gauss58]

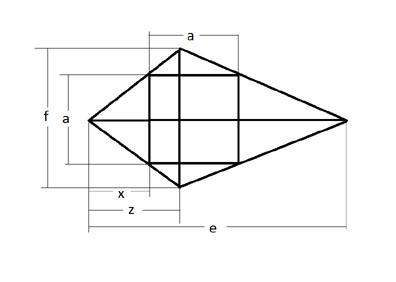
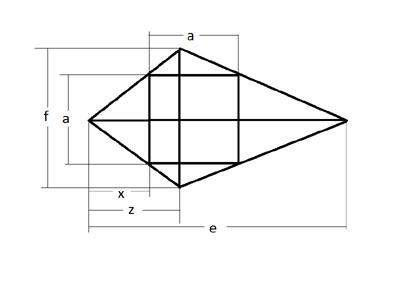
Eine rechnerische Lösung kann ich Dir anbieten:

gegeben:

e = Diagonale 1 (Symmetrieachse)

f = Diagonale 2

z = Abschnitt auf e vom linken Eckpunkt bis zum Schnittpunkt der Diagonalen

gesucht:

x = Abschnitt auf e vom linken Eckpunkt bis zum Beginn des Quadrates

a = Seitenlänge Quadrat

(1) (a/2) / x = (f/2) / z

(2) (a/2) / (e – a – x) = (f/2) / (e – z)

-----------------------------------------

x = e * z / (e + f)

a = f * e / (e + f)

Interessanterweise ist a nur abhängig von den beiden Diagonalen.