Wie rechnet man diese Aufgaben (Quadratische Funktionen)?
Ich schreibe morgen ne Matheklausur und diese beiden Aufgaben sind als Übung angegeben, ich verstehe sie aber nicht. Mir sind ein paar Taschenrechner-Befehle bekannt (polyRoots, nSolve, Define). Kann mir jemand sagen wie man sowas rechnet?
3 Antworten
links und rechts unten am Boden :

::::::::::::::::::::::::::::::::::::::::::::::::::::::
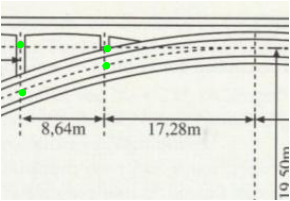
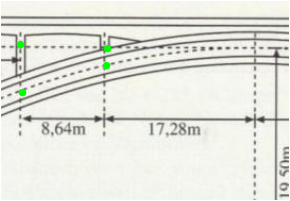
mit x = -17.28
und x = -17.28-8.64 = -25.93
usw
werden die grünen Höhen bestimmt
Höhe = a*-(17.28)
das sind die Pfeilerhöhen ( ohne Vorzeichen natürlich )

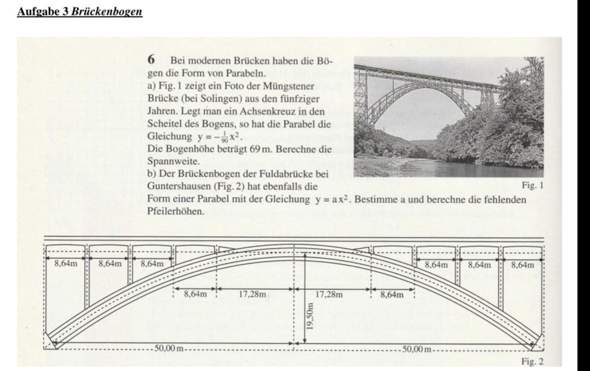
Hi, bei Aufgabe 6a wird ja die Spannweite gefragt, quasi die Länge der Brücke. Du hast eine Gleichung, die dir den Brückenverlauf anzeigt und du hast die Höhe gegeben. Nun einfach Gleichung gleichsetzen mit 69m um herauszufinden, an welcher Stelle die Brücke so tief ist. Das ist nämlich das Ende der Brücke, nämlich ganz links und ganz rechts. So kommst du auf die Werte -78,8 und +78,8. Da dies vom Nullpunkt aus, also der Mitte die Abstände nach links und rechts sind, du aber den gesamten Abstand brauchst, multiplizierst du 78,8 einfach mit 2 und bekommst als Ergebnis für die Länge 157,6
6a
69 -1/90 * x^2 = 0
x^2 = 6210
x = 78,80
Also beträgt die Spannweite 157,61 m
Ich glaube die 51,84 stimmen nicht, für die Höhe 19,5m muss man schon 50 nehmen
An der Stelle x=51,84 geht es noch weiter runter als 19,5m. Die Tiefe beträgt dort nämlich 20.96m
y = 19,50 = ax^2 mit x = 4 * 8,64 + 17,28 = 51,84
a = 19,50/51,84^2 = 7,256E-3
y = 7,256E-3 * 17,28^2 = 2,17
y = 7,258E-3 * (17,28 + 8,64)^2 = 4,88
u.s.w.