Wie löst man das Rätsel?
Weiß jemand wir man das Rätsel ohne 2 mal über eine Seite zu kommen löst?

Was ist hier die Aufgabe das ist nur ein bild
Man muss es mit einem Strich zeichnen ohne doppelt über eine Seite zukommen so wie beim Haus vom Nikolaus
2 Antworten
ich würde sagen gar nicht.
deswegen gibts ja das beliebte "Haus vom Nikolaus", was die Sache durch die 2 Dachseiten löst und nun jede Seite und Diagonale wirklich nur einmal benötigt und in einem Rutsch zu zeichnen ist.
ich habe ein Video, warum es NICHT funzt. du darfst schlicht nicht ausschließlich ungerade Anzahl von Kanten in den Ecken haben, weshalb Nikolaus auch die 4er Ecken braucht. cooler Kram !
https://www.youtube.com/watch?v=ST2XpL6o4kk
Man muss es mit einem Strich zeichnen ohne doppelt über eine Seite zukommen so wie beim Haus vom Nikolaus
Da gibt es keine Lösung.
=============
Begründung: Ich habe dazu mal ein kleines Python-Skript geschrieben.
(Vorweg: Das Skript ist nicht gerade effizient geschrieben. Aber es muss ja jetzt auch nicht effizient sein, sondern mir einfach nur die entsprechenden Lösungen liefern, wenn es welche gibt.)
from itertools import product, pairwise
erreichbare_Punkte = {0: [1, 2, 3, 4],
1: [0, 2, 4],
2: [0, 1, 3],
3: [0, 2, 4],
4: [0, 1, 3]}
streckenzahl = 8
anzahl_lösungen = 0
for p in product(range(5), repeat=streckenzahl+1):
keine_nullstrecke = True
erreichbarkeit = True
strecken_nicht_doppelt = True
for i in range(streckenzahl):
if p[i] == p[i+1]:
keine_nullstrecke = False
break
if not p[i+1] in erreichbare_Punkte[p[i]]:
erreichbarkeit = False
break
if (p[i], p[i+1]) in pairwise(p[:i+1]):
strecken_nicht_doppelt = False
break
if (p[i+1], p[i]) in pairwise(p[:i+1]):
strecken_nicht_doppelt = False
break
if keine_nullstrecke and erreichbarkeit and strecken_nicht_doppelt:
anzahl_lösungen += 1
print(p)
print(f"Es wurden {anzahl_lösungen} Lösungen gefunden.")
Idee dahinter: Ich bezeichne einige Punkte entsprechend der folgenden Skizze mit Zahlen.
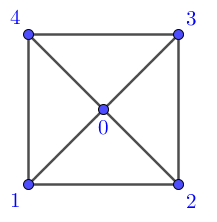
Nun muss ich einen entsprechenden Weg bestehend aus 8 Strecken (p0, p1), (p1, p2), ..., (p7, p8) finden, wofür ich einfach alle Möglichkeiten mit p0, p1, ..., p8 ∈ {0, 1, 2, 3, 4} durchgegangen bin und jeweils geschaut habe, ...
- ... ob ich bei den Teilstrecken (p0, p1), (p1, p2), ... tatsächlich immer vorangegangen bin oder irgendwo stehen geblieben bin. Wenn beispielsweise p3 = p4 wäre, wäre ich in dem Schritt stehengeblieben, sodass ich dem Weg folgend insgesamt weniger als 8 Teilstrecken gezeichnet hätte. („keine_nullstrecke“ im Skript)
- ... ob die Teilstrecken, die ich gehen möchte, tatsächlich in der Zeichnung vorhanden ist. („erreichbarkeit“ im Skript)
- ... ob ich eine Teilstrecke nicht zuvor schon gegangen bin. („strecken_nicht_doppelt“ im Skript)
Wenn das alles passt, soll der entsprechende Weg als Lösung ausgegeben werden.
Ergebnis, welches mir das Skript geliefert hat:
Es wurden 0 Lösungen gefunden.
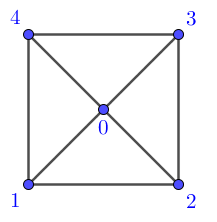
dann hatte ich mit dem Skript auf meinem Kopf ja den richtigen Riecher , bzw . jetzt wird es ganz klar , wofür der Niko das Dach braucht !
Bin mir sich das es da eine gibt find das Video aber nicht mehr