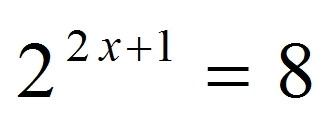Wie löse ich Exponentialgleichungen ohne Logarithmieren?
Guten Abend, leider ist meine Nachhilfe ausgefallen und daher sind mehrere Probleme aus dem Matheunterricht dieser Woche nicht behandelt worden. Ist stelle mir die Frage wie ich Exponentialgleichungen ohne Logarithmieren lösen kann. Ich würde mich freuen wenn mir jemand die Lösung zur Aufgabe a und b aus dem Bild mit Lösungsweg und kurzer Erklärung schreiben könnte Aufgabe a) 2^2x+1=8 b) 3^3x-6=81
3 Antworten
a) 2^(2x+1) = 2³ und im Vergleich 2x+1 = 3 und b) schaffst du!
Wie oft geht die 3 in die 9, bzw. in die 81?
Wenn Du es weißt, dann Stelle gleiche Basen her, links und rechts, vom Gleichheitszeichen.
Dann kannst Du die Exponenten vergleichen.
Nachschlagen kannst Du unter "Vergleich der Exponten" oder unter "Exponentenvergleich"
Du hast ja sicher einen Mathematik-Duden oder den dtv Atlas zur Mathematik *heißer Tipp*
😉
Du meinst sicher
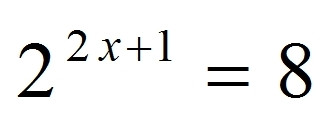
Da man bei GF nicht gescheit formatieren kann, mußt Du Klammern setzen:
2^(2x+1) = 8
Ohne die Klammern bedeutet es 2^(2x) + 1 = 8