Wie geht diese Textaufgabe zum Sinussatz ?
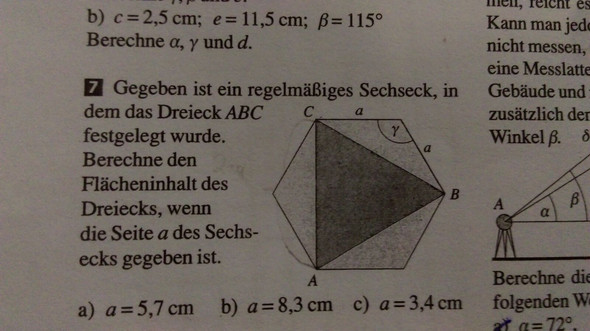
Hallo, ich mache gerade meine Hausaufgaben und komme bei dieser Aufgabe nicht weiter. Thema: Sinussatz. Ich verstehe nicht wie ich andere winkel Berechnen soll, ohne einen Winkel zu kennen.. gegeben habe ich nur a= 5,7cm. Hab noch ein Bild der Aufgabenstellung angegangen. Nicht falsch verstehen, ich will nicht das ihr meine Hausaufgaben macht, ich komme nur wirklich nicht weiter.. Vielleicht habt ihr ja einen tipp ohne das genaue Ergebnis zu nennen ?
2 Antworten
Hallo,
Du kannst aus der Angabe, daß es sich um ein regelmäßiges Sechseck handelt, den Winkel Gamma berechnen, denn die Innenwinkelsumme eines Sechsecks beträgt 180°*(n-2), also 180°*4=720°.
Dann entfällt auf jeden einzelnen der sechs gleichen Innenwinkel 720/6=120°.
Nun kannst Du eine Seite des gleichseitigen Dreiecks berechnen, denn nach dem Sinussatz verhält sich BC/sin (Gamma) wie a zum Sinus des gegenüberliegenden Winkels, der 30° beträgt, denn das Dreieck oberhalb der Seite BC ist gleichschenklig und somit die Basiswinkel gleich groß.
Da für Gamma bereits 120° weg sind, bleiben für die beiden anderen Winkel zusammen 60° (Summe der Winkel eines Dreiecks=180°), für jeden demnach 30°.
Du kannst BC auch über den Kosinussatz berechnen, da Gamma und die Seiten, die Gamma einschließen, bekannt sind.
Die Fläche des gleichseitigen Dreiecks ABC berechnest Du dann über die Formel a/2*Höhe und die Höhe über den Satz des Pythagoras:
h²=(BC)²-(BC/2)², da BC=AB=AC
Herzliche Grüße,
Willy
9,87 für BC ist korrekt.
Die Höhe berechnest Du nach dem Satz des Pythagoras:
(Höhe von A auf BC)²=(AB)²-(BC72)², also 9,87²-(9,87/2)²
Das ergibt etwa 73 cm² und die Wurzel daraus etwa 8,54 cm.
Der Flächeninhalt des Dreiecks ist demnach 8,54*9,87/2 cm²
Also nicht h/2, sondern BC/2 mußt Du rechnen, obwohl: Ist wurscht wegen Kommutativgesetz.
Willy
Nennen wir die Dreiecksseite zwischen B und C b und den Winkel zwischen b und A alpha. Dann gilt laut Sinussatz: b/sin (gamma)=a/sin (alpha). b ist gesucht, a schon gegeben. Du brauchst jetzt noch die Winkel alpha und gamma.
Da das Sechseck gleiseitig ist, ist auch das eingezeichnete Dreieck gleischseitig. Die Winkel in einem gleichseitigen Sechseck betragen 120°, die in einem gleischseitigen Dreieck 60°.
Jetzt sieh dir Punkt C an. Dort befindet sich eine Spitze des Dreiecks. Die beiden Winkel auf jeder der Seite sind gleich groß. Du weißt, dass der gesamte Winkel in C 120° beträgt, der in der Dreiecksspitze 60°.
Kommst du damit weiter?
Ich hoffe ich konnte dir weiterhelfen :)
Ja, erstmal danke dir, hat mir weitergeholfen b ist ja dann einfach sin(120)/b=sin(30)/5,7 bzw. 9,87cm. Das bedeutet dann das alle seiten 9,87cm lang sind richtig ? Wenn ich dann aber den Flächeninhalt berechnen will, brauche ich ja noch die Höhe, ist diese in dem Fall dann 11,4cm (2*5,7cm), oder wie kann ich die höhe bestimmen ? Mit den 11,4cm als wert für die Höhe bekomme ich als Flächeninhalt(A= b*h/2) 56,26 raus. Ist das so richtig ?
Danke dir, sehr hilfreich :D. BC ist ja dann einfach sin(120)/BC=sin(30)/5,7 bzw. 9,87cm. Das bedeutet dann das alle seiten 9,87cm lang sind richtig ? Wenn ich dann aber den Flächeninhalt berechnen will, brauche ich ja noch die Höhe, ist diese in dem Fall dann 11,4cm (2*5,7cm), oder wie kann ich die höhe bestimmen ? Mit den 11,4cm als wert für die Höhe bekomme ich als Flächeninhalt(A= BC*h/2) 56,26 raus. Ist das so richtig ?