Wie geht diese Mathe Aufgabe ?
Zwischem zwei 5m hohen Masten, die 12m voneinander entfernt auf verschiedenen Strassenseiten stehen,soll in der Mitte der strasse eine Laterne aufgehängt werden. Das Stahlseil zur Befestigung ist 12,10m lang. Wie hoch dürfen Fahrzeuge maximal sein, damit sie gefahrlos unter der Laterne hindurchfahren können ?
4 Antworten
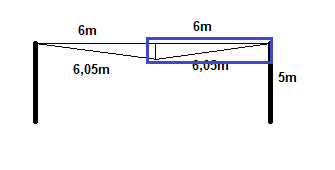
Ich kann im Kommentar kein Bild einfügen, deshalb kriegst du eine neue Antwort. Siehe Bild.
Links und rechts sind die Pfeiler, die jeweils 5m hoch sind. Die beiden Linien, wo 6m dransteht, sind der gesamte Abstand zwischen den Pfeilern. Die Linien, wo 6,05m dransteht, sind das Seil. Das blau umrandete ist ein rechtwinkliges Dreieck und wie du's rechnest, steht in meiner anderen Antwort.
Kann man nicht, denn dazu müsste gewährleistet sein, dass das Stahlseil exakt am allerobersten Ende der beiden Masten befestigt ist. Anders ausgedrückt; in welcher Höhe BEI DEN MASTEN ! exakt soll das Stahlseil aufgehängt werden? Außerdem: wie lang ist denn die Laterne? Wieviel cm? Die hängt ja dann runter, und das muss man wissen. Ansonsten würde ich schlichtweg sagen: gehen wir mal davon aus, dass die Stahlseile ganz oben an den Masten angebracht werden, diese nicht durchhängen (Achtung: von dem Durchmesser und dem Material des Seiles war auch nicht die Rede), die Autos immer rechts und links an der Laterne vorbeifahren können (hängt ja in der Mitte) NATÜRLICH 4,50 meter- das nenne ich dann gefahrlos.
die aufgabe ist wirklich dumm aber steht in meinem Mathebuch :D
Er wollte nicht wissen, wie die Lösung geht, sondern wie die Aufgabe geht
Von dir kommt nichts hilfreiches, nur Geschwafel. So von wegen: Wie die Aufgabe geht, hast du selber geschrieben. Aber offentsichtlich bist du meiner Meinung, was die Lösung an sich angeht. Die Aufgabe selber ist kompetter Unfug.
Dafür müsste man eigentlich die Kettenlinie berechnen (https://de.wikipedia.org/wiki/Kettenlinie_(Mathematik)). Da ich das aber nicht auf die Schnelle lernen kann mach ichs mir ein bisschen einfacher und benutze Trigonometrie.
Man kann das Seil in zwei Seiten aufteilen, die jeweils ein Dreieck bilden. Die 6 Meter zwischen einem Pfeiler und der Mitte zwischen den Pfeilern wären dann eine Kathete und 6,05 Meter von einem Ende des Seils bis zur Mitte des Seils wäre die Hypotenuse. Die fehlende Seite des Dreiecks kann man dann ganz einfach mit dem Satz des Pythagoras ausrechnen. Das was da rauskommt, kannst du dann von den 5 Metern Pfeilerhöhe abziehen und du hast den niedrigsten Punkt, den das Seil erreichen kann.
danke aber versteh ich irgendwie nicht ich find da kein sinnvolles rechtwinkliges dreieck
Nur so ein Tipp:
Du hast ein gleichschenkliges Dreieck mit der Höhe 0,10 m.
Ohaa danke :D