Wie teile ich die Figure?
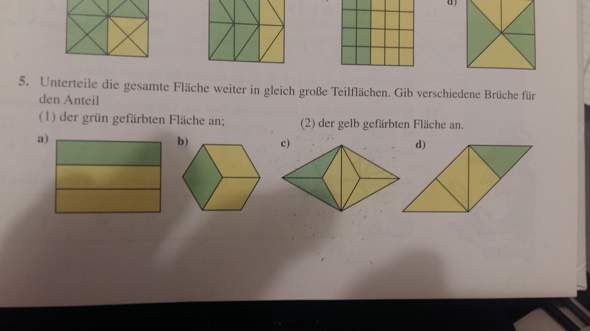
No 5 c
der erste Bruch ist (2/6) erweiterung mit 2 bekommt man (4/12) da sieht man beim
zwietn Bild. Die Frage jetzt wie kann ich die Figur noch um 2 erweitern , nämlich
(8/24) ? wusste wie und wo teil ich die Figure , dmit der Bruch (8/24) raus kommt
hier

4 Antworten
Ich habe jetzt nur die Dreiecke aus dem 4/12 Teil in 8/24 geteilt.
Das funktioniert aber nur dann, wenn bei der ursprünglichen Figur die Diagonalen das Verhältnis 2:1 haben, wenn sie also doppelt so breit wie hoch ist.


Schachapapa, ich möchte sehr gern men Logik verstärken und verbessern , kannst du sol wohl Bücher also auch Web Seite und Videos empfehlen um meine Logik zu verbesser: ich möchte mich später mit Informatik beschäftigen( Umschulung oder Studium)
Sie sind nicht kongruent, aber die Flächen sind gleich. Betrachte das obere braune Dreieck und das direkt darunter angrenzende, bei dem die drei Seiten ungefähr gleich lang sind. Die beiden Dreiecke haben eine Seite gemeinsam und die jeweilige Höhe ist ebenfalls gleich. Die Winkel und übrigen Seitenlängen sind allerdings verschieden.
versteh nicht alles ganz ,(die jeweilige Höhe ist ebenfalls gleich. )?
Verstehe die Aufgabenstellung nicht, die Teilflächen aller Figuren sind jeweils schon gleich groß.
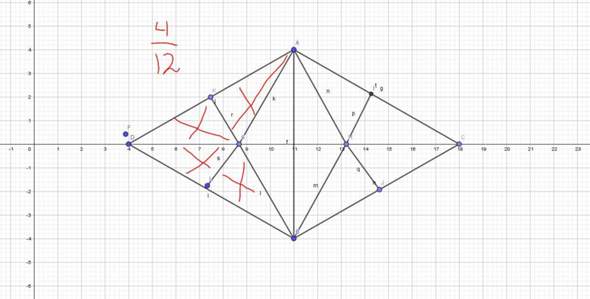
ich möchte die Figur c auf den Bruch erweitern (8/24) aber wie kriege ich 24 gleiche große Teil ? ich habe in Bild 2 den Bruch von(2/6) auf (4/12) und habe die Dreiecke gezeigt , jetz wie und wo teile ich weite ,damit ich den Bruch (8/24) erhalte?
Ich glaube, wir haben hier beide Quatsch gemacht und das ist alles Unsinn.
Bei der ursprünglichen Figur ist der grüne Teil nur dann zwei Sechstel, wenn die einzelnen Dreiecke gleich groß sind. D.h. die Seitenlängen des Gesamtvierecks (in meiner Zeichnung also UR, RV, VS und SU) müssen genauso lang sein wie die kurze Diagonale RS. Dann hast du zwei nebeneinanderliegende gleichseitige Dreiecke SRU und SVR mit den Umkreismittelpunkten W und Z, d.h. es gilt WR=WU=WS = ZR=ZV=ZS.
In einem gleichseitigen Dreieck mit der Seitenlänge a hat die Höhe die Länge a * wurzel(3)/2. Deshalb kann man die Eckpunkte U und V nicht bequem auf Koordinaten zeichnen, denn UV = wurzel(3) * RS
Anschließend kann man lustig halbieren und es sieht am Ende nicht schief aus.


Das Dreieck BCW hat die gleiche Fläche wie das Dreieck CBR, sie haben die Seite CB gemeinsam und die Höhe auf CB durch W ist ebenso lang wie die Höhe auf CB (verlängert) durch R.
Fazit:
Die eigentliche Aufgabe war einfach nur, die vorhandenen Dreiecke einmal zu halbieren, um 2/6 auf 4/12 zu erweitern. Das wäre einfach gewesen.


Die Aufgabenstellung sieht wohl nur eine einmalige Halbierung vor. Das ist einfach und das hast du schon gemacht.
Wenn du diese rechtwinkligen Dreiecke noch einmal halbieren willst, kannst du den Mittelpunkt einer der beiden Katheten mit der gegenüberliegenden Ecke verbinden. Die beiden Hälften sind dann aber nicht kongruent.

Das obere Dreieck kann man anscheinend bequem weiter halbieren. Das liegt aber wohl daran, dass ich zufällig günstige Seitenlängen gewählt habe.
Für dieses Beispiel passt das aber. Im nächsten Schritt bekommst du dann wieder lauter kongruente Dreiecke.

Ich sehe gerade, dass das obere Beispiel genau nicht eine Kathete, sondern die Hypothenuse halbiert. Passt aber wohl trotzdem.
du siehst in Teil c ist die figur hat insgesamt 6 gleich gross Teile ist, 2 grün und 4 gelbe ich habe im zweiten Bild den von 2/6 auf 4/12 also 4 rote und 8 wieße , jetzt möchte´die Figure weiter unterteilt ,, also 8/32 , 8 rote und und 24 weiße . is t das möglich , und wie? esg geht um nicht den Bruch sonderen möchte die Figure wie sie in 32 gleich gross Teile unterteilt(8 rot und 24 weiße). wenn geht möchte das sehen
Man kann in Unterantworten anscheinend keine Bilder hochladen, siehe andere Antwort.
aber diese Teile scheinen mir nicht ganz gleich oder? ich meine jede 4 Teil sind identisch und die anderen 4 Teil sind von diese $ teile nicht ganz gleicg oder? sehen größer