Widerstandsmatrix erklären?
Hi,
wie kommt die Widerstandsmatrix bei der Mehrfachleitung zu stande? Was ist R_0 und warum steht bei den Diagonalen R_n+R_0?

2 Antworten
R0 ist der Wirkwiderstand der Bezugsleitung im betrachteten System (Mehrfachleitungen, d.h. n+1 parallele Leiter). Für üblich wird willkürlich eine der Leitungen als Bezug genommen.
Die restlichen Leiter werden mit den Indizes 1 bis n bezeichnet. Die Widerstandsmatrix ( n x n) leitet sich dann von den Betrachtungen der jeweiligen Spannungen und Ströme der Leitungen ab, für die es ebenfalls eine Matrix gibt.
Solche Matrizen lassen sich auch für die Induktivitäts- und Kapazitätsbelage aufstellen.
Das liegt vermutlich an den Gegenkapazitätsbelägen, die zwischen den Leitungen entstehen und in der Matrix für die Querimpedanzbeläge dann mit negativem Vorzeichen landen. Die Summe entsteht bei den Querimpedanzen bzw. der Kapazitäten dadurch, dass sich nicht nur zwischen Leitung n und der Bezugsleitung, sondern auch unterhalb der Leiter sich Kapazitäten bilden.
Ohne den Kontext zu zeigen hat das keinen Sinn.
Monentan sehe ich das:
Und hier ist
Es gibt aber nicht "die" Mehrfachleitung, du musst schon schon sagen, worum es geht.

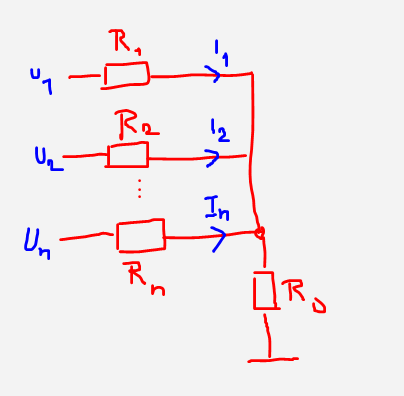
Ich habe hier ein Schaltbild einer Mehrfachleitung. Ich habe ja mit 0 den Bezigsleiter und einen Basiswiderstand R_0? Schreibt man R_n+R_0 weil der Basiswiderstand auf alle Leitungen wirkt?
Diese Schaltung hat aber mehr als deine Widerstandsmatrix. Wo sind bei dir die G(m,n) dieser Schaltung? Ich identifiziere in der Matrix nur die G(m,0) und die R(m). Abgesehen davon fehlen die L und C...was jetzt? Kannst du mal die vollständige Aufgabe posten?
Solange du nicht klar sagst was du machen willst kannst du dir keine sinnvolle Antwort erwarten. Aus deinem neuen Bild sehe ich ein n-Leitungssegment mit Ein- und Ausgängen und differenziellen Belägen. Es macht daher Sinn eine Matrix aufzustellen wo die Ausgangs- mit den Eingangsgrößen verknüpft sind, z.B.
(u1', u2', ... i1' i2'...) = A*(u1', u2', ... i1' i2'...)
A wäre dann die inverse Kettenmatrix.
Du kannst aber auch ansetzen
(u1, u2, ... u1' u2'...) = Z*(i1, i2, ... i1' i2'...)
Z wäre dann die Impedanzmatrix.
Es gäbe dann auch noch andere Formen der Beschreibung...
Du sagst aber nicht worum es geht und in welcher Form du das Leitungssegment beschreiben sollst. Deine erste Matrix hat mit dem Bild jedenfalls nichts zu tun.
"Solche Matrizen lassen sich auch für die Induktivitäts- und Kapazitätsbelage aufstellen."
Warum hat man hier bei der Kapazität diese Summenschreibweise und das negative Vorzeichen?
https://ibb.co/TBw1HXY