Was wäre hier die Höhe?
Hallo,
ich muss diese Aufgabe lösen und wollte fragen, was nehme ich hier als Höhe ? 2 ? Oder 4 ? Kann man das auch komplett drehen?
Viele Grüße

4 Antworten
Du hast die Antwort ja schon erhalten.
Von mir als Ergänzung nur die Info, dass du den Körper selbstverständlich beliebig drehen kannst, wenn du willst. (Ob das zur Ermittlung des Volumens hilfreich ist, ist eine andere Frage.)
Stell dir vor, du hast einen Tetrapak mit einem Liter Milch. Oder ein Flasche mit einem Liter Wasser. Oder eine Tasse mit 250 ml Kaffee.
Natürlich kannst du diese Objekte beliebig drehen, ohne dass sich ihr Volumen ändert.
(Nur bei der Tasse wird es kritisch, weil bei ungeschickter Drehung der Inhalt nicht in der Tasse bleibt! 😛)
Die Ausmessungen eines geometrischen Objekts, egal ob eindimensional (Länge), zweidimensional (Fläche) oder dreidimensional (Volumen) ändern sich doch nicht, wenn du es hin und her drehst. (Das wäre nur der Fall, wenn du es verformst.)

das sind die Seiten für die Formel
daher ist die Höhe 3 !
Man bezeichnet den ABSTAND der beiden Parallelen 2 und 4 beim Trapez als HÖHE.
Und es ist daher egal wie das Trapez "liegt"
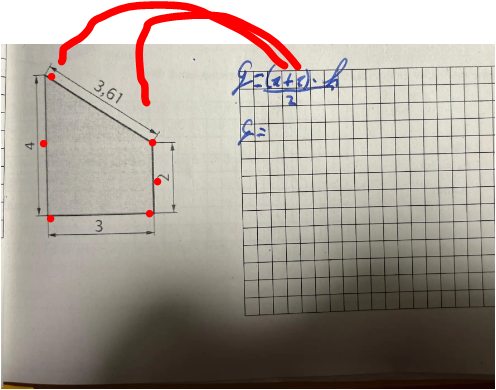
Du nimmst die falsche Seite, Du kannst auch die Formel für ein Trapez nehmen und als Höhe 3 nehmen, da sich die beiden anderen Längen parallel gegenüber stehen und rechtwinklig zur Seite mit 3mm länge stehen, das heißt, die Seite mit 3 mm bildet die Höhe ab.
Du kannst also:
nehmen und erhältst die Fläche. Das Volumen wird gesucht, die Werte sind bisher in mm und mm².
Du kannst Mittelwert nehmen, wenn du die Fläche brauchst. 2+4)/2=3