Von einer Zuordnung eine Funktionsgleichung erstellen?
Hallo,
Ich habe eine Frage. In einer Matheaufgabe steht : Eine Softfirma plant für die Ersteölung eines Computerprogramms 12 Programmierer für 15 Arbeitstage. Erstelle für die Zuordnung ANZAHL DER PROGRAMMIERER - >ANZAHL DER ARBEITSTAGE die Funktionsgleichung
Dankeschön im Voraus

G
Kannst du ein Foto der (gesamten) Aufgabe hochladen?
Wie macht man das
Bild oder Screenshot machen und dann unten links bei deiner Frage auf "Frage ergänzen" gehen und oben in der Leiste das Bild (ist ein Symbol) antippen und auswählen
Hab gemacht
1 Antwort
Für 15 Arbeitstage werden 12 Programmierer benötigt. In dem Kontext zur Aufgabe bedeutet es, dass bspw. für 30 Arbeitstage nur 6 Programmierer benötigt werden. Deine antiproportionale Zuorndung "Anzahl der Programmierer —> Anzahl der Arbeitstage" sieht also wie folgt aus:
f(x) = 180 / x
Denn für die Antiproportionalitätskonstante k gilt A = k / B, also k = A * B, und damit konkret
k = 15 * 12 = 30 * 6 = ... = 180.
Hier unten ist noch der Graph der Funktion f.
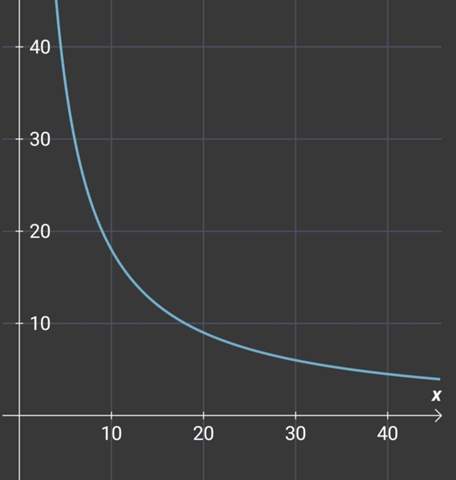
___
Ergänzung
___
Bei Nr. 4 musst du die Punkte in f einsetzen und nach k auflösen, also bei einem Punkt (x|y) erhälst du f(x) = y = k / x <=> k = y * x.
a) P(3|4): 4 = k / 3 <=> k = 4 * 3 = 12
b) P(8|0.5): 0.5 = k / 8 <=> k = 8 * 0.5 = 4
c) P(–5|–1): –1 = k / (–5) <=> k = –5 * (–1) = 5
d) P(–2|4.5): 4.5 = k / (–2) <=> k = –2 * 4.5 = –9
Die Funktionswerte kannst du einfach berechnen, indem du dein ausgerechnetes k in f(x) = k / x einsetzt und dann die gegebenen Stellen x = 1; –1.4; –1/2 einsetzt.
a) f(1) = 12 / 1 = 12
f(–1.4) = 12 / (–1.4) ≈ –8.6
f(–1/2) = 12 / (–1/2) = –24
b) f(1) = 4 / 1 = 4
f(–1.4) = 4 / (–1.4) ≈ –2.6
f(–1/2) = 4 / (–1/2) = –8
c) f(1) = 5 / 1 = 5
f(–1.4) = 5 / (–1.4) ≈ –3.6
f(–1/2) = 5 / (–1/2) = –10
d) f(1) = –9 / 1 = –9
f(–1.4) = –9 / (–1.4) ≈ 6.4
f(–1/2) = –9 / (–1/2) = 18
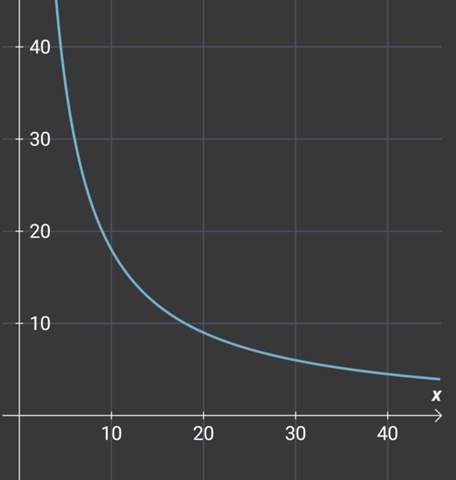
Dankeschön, könntest du mir vllt auch direkt die nr 4 erklären