Vandermonde Determinante, Beweis, kann mir einer beim Verständnis helfen?
Zu Beweisen ist :

Bewis:

Zunächst, im Beweis steht, dass der erste Block die gleiche Determinante wie der zweite block hat...
Ich habe doch beim ersten Block die 1, also erster Block hat Determinante 1, da nur da die 1 steht.
Der zweite Block ist doch das hier orange markierte:

oder? Meint man das mit zweiten Block? Wenn ja, warum hat die jetzt automatisch auch Determinante von 1?
Und danach verstehe ich hier nicht:

Wie genau hat man diese Umformung gemacht? Ich ziehe x1-fache der n-1-ten Spalte von der n-ten Spalte ab? Was meint man genau damit?
Und danach steht " Mit Induktion erhält man ...". Muss ich bei dem Beweis nicht die Induktion noch mit schreiben? ALso damit meint man wahrscheinlich einen Induktionsbeweis, muss man den nicht noch beifügen?
Und nun:
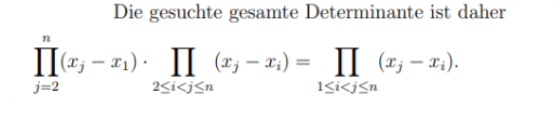
Das verstehe ich auch garnicht wie kam man nun hierhin? Zu dieser Gleichung?
1 Antwort
Ne, der 2. Block ist das was unterhalb der 1. Zeile und rechst von der 1. Spalte steht. Der 1. Block ist die 1x1 Einheitsmatrix. Es gibt eine Formel für Blockmatrizen und Determinante, die da angewendet wird.
Mit „das x_1-Fache der n-1. Zeile von der n. Zeile abziehen“, ist gemeint, dass die Elementarmatrix R_{n-1,n}(-x_1) vom Typ 1 mit der Matrix rechts-multipliziert wird. Die Determinante dieser Matrix ist 1, daher ändert die Multiplikation nicht die Determinante.
https://de.m.wikipedia.org/wiki/Elementarmatrix
Die Gleichung gilt, kannst du nachprüfen. Auf die linke Seite kamen sie eben mit Induktion. Sie haben das Problem auf das Problem einer kleineren Matrix reduziert, damit können sie die Induktion anwenden.
Studierst du Mathematik?
v_{n-1} der (n-1)-te Spaltenvektor und v_n der n-te Spaltenvektor, dann ergibt sich der n-te Spaltenvektor nach Umformung durch:
v‘_n = v_n - x_1 • v_{n-1}.
Rechne mal nach, dann wirst du sehen, dass (x_2^{n-2} , … , x_n^{n-2}) übrig bleibt.
v_{n-1} bleibt in dieser Umformung natürlich erstmal unverändert.
Danke, das an sich, also dass ich so rechnen muss: "v‘_n = v_n - x_1 • v_{n-1}" habe ich direkt verstanden, ich weiß nur nicht wie ich das rechnen soll, da ich nicht weiß wie die v_{n-1} Spalte aussieht? die letzte Spalte der Matrix, also v_n ist ja die Spalte mit x^(n-1) ist dann v_{n-1} die Spalte mit x^(n-2)?
Sorry, hab den zweiten Block falsch markeirt sollte natürlich ohne erste Zeile und 1 Spalte sein ....
Aber hat sich dann geklärt, erster Block mal zweiter Block, habe dann nur Determinante von ´zweiten block als Determinante der Matrix, da erster Block Determinante 1 hat und somit keine Wirkung.
Das mit dem x-1-fachen habe ich nicht ganz verstadnen. ALso klar Elementarmatrix, einfahc Diagonale multiplizieren, daher Determinante=1 und verändert nichts beim multiplizieren.
Aber verstehe nicht, wie durch das multiplizieren des x-1-fachen etc. die daraus folgende Matrix entsteht?
Studiere Wirtschaftsinformatik, nicht Mathematik, also Informatik halt.