Punktprobe des Schnittpunktes 2 linearischer gleichungen?
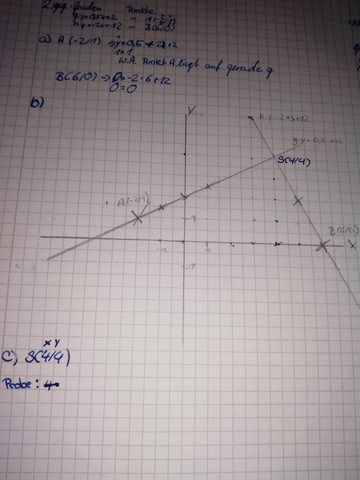
Hallo also ich möchte wissen wie man aus den Gleichungen g: y=0,5x+2 und h: y=-2x+12 und dem S(4/4) die Probe rechnen kann .
4 Antworten
Du setzt den x-Wert in jede Gleichung ein und überprüfst, ob y = 4 herauskommt.
x = 4
g(4) = 0,5*4 + 2 = 2+2 = 4
h(4) = -2*4 + 12 = -8 + 12 = 4
g(4) = h(4) = 4 für x = 4
Den Punk (x/y) Wert in X und Y einsetzen bei beiden Gleichungen, dann beide Seiten gegenüberstellen, also aus y1=(Gleichung1) und y2=(Gleichung2) wird zu Gleichung1= Gleichung 2
Dann eifnach ausrechnen und am Ende steht dort dann
X=_ S>timmt dieses X mit deinem Punkt überein, hast du alles richtig gemacht
y=y
=> 0,5x+2=-2x+12
0,5x+2=-2x+12 I +2x
2,5x+2=12 I -2
2,5x= 10 I :2,5
x = 4
Ab hier gibt es 2 Varianten
1.
y= 0,5x+2 I einsetzen
y= 0,5 *(4)+2
y=2+2
y=4
2.
y=-2x+12 I einsetzen
y= -2*(4)+12
y= -8+12
y=4
Probe? - ganz simpel: setze in beiden(!) Gleichungen den x-Wert des Punktes ein und berechne den y-Wert (von beiden Gleichungen). Sind diese gleich (und zwar dem des Punktes), liegt der Punkt auf beiden Geraden.