Projektion Google Earth?
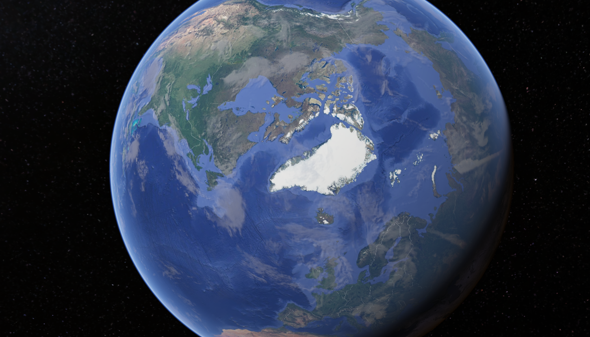
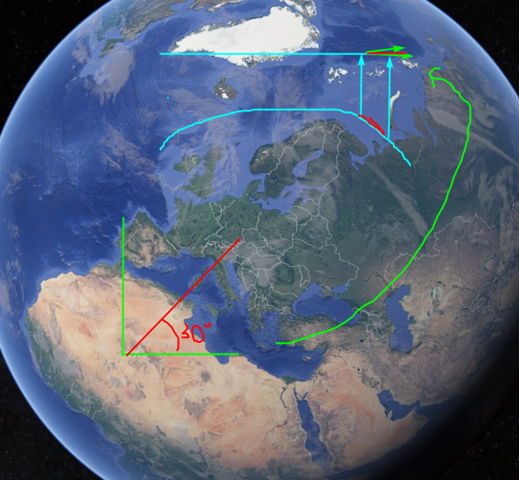
Ferner sind Winkel auf der Karte falsch , Längen und Flächen auch.
Gibt es noch andere Projektionen die für 3D Kugeln , die in Programmen verwendet werden bzw. eigentlich sind es ja Kreise auf meinem 2D Bildschirm.
Hier gibt es ein Video:
Was für eine Projektion ist das, wenn der Globus am Anfang dargestellt wird?
https://www.youtube.com/watch?v=E43g5EMxaTg
2) Eine Frage habe ich noch zu den Maßstäben:
Auf Weltkarten ist häufig ein Maßstab angegeben.
Was für ein Sinn hat so eine Maßstabsangabe, wenn der Maßstab höchstens nur in einem ganz bestimmten Bereich gilt und zwar dort wo z.B. der Zylinder bei der Mercatorprojektion die Oberfläche des Mittelmeridians berührt.

und selbst bei großen Maßstäben haben wir Längenverzerrung, wenn auch kaum merklich. Was für einen Sinn haben also die falschen Maßstabsangaben , vorallem bei Weltkarten. Wie soll der durchschnittliche Nutzer einer Karten wissen ,ab welcher Kartengröße der Maßstab nicht mehr überall gilt? bzw. ab wann die Abweichungen in Richtung der Ränder zu stark sind ,sodass signifikante Längenverzerrungen auftreten, wenn er z.B. eine Strecke auf der Karte vermessen will.
3)
Wie rechnet Google die Strecken aus?
4) Strecken bei UTM Koordinaten sind auf 100m in Echt ca. 3,3 cm zu Kurz beim Mittelmeridian der Projektion , richtig? Wie kann man mit so falschen Maßen ordentlich Dinge vermessen?
2 Antworten
Das ist einfach ne 3D Kugel mit Textur. Da wird nicht projeziert oder umgerechnet würde ich sagen.
"Die Textur muss ja nach bestimmten Maßen erstellt werden. "
NMach den reellen Maßen natürlich.
Es wird die "Flughhöhe" angegeben.
Du bringst das Problem der Projektion einer Kugel auf ein ebene Fläche ins Spiel. Das kommt aber hier gar nicht zum Tragen.
und genauso muss ja auch die Flächengröße festgelegt werden. Afrika ist in Google Earth ja nicht zufällig in dem verhältnis dargestellt z.B. zu Europa. D.h. irgendeine Gesetzmässigkeit, ein Verhältnis bzw. eine Berechnung , eben eine Projektion von der realen Kugel auf den 2D Auschnitt auf dem Bildschirm. ( für uns eben als 3D Bild /Kugel durch die Maße wahrnehmbar) , wird es gegeben haben.
Mein Bildschirm ist doch eine ebene Fläche, oder nicht? ^^ Genau wie eine klassische Karte.
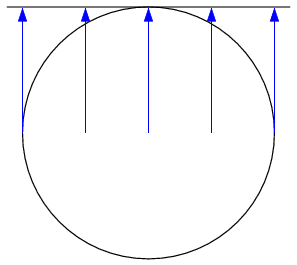
Ist das die Orthografische Azimutalprojektion?
Nein, senkrechte Umgebungsperspektive - Forografiere einen Globus, dann solltest Du das gleiche Resultat bekommen.
2: Da der Maßstab sich verändert, sieht die Maßstabsangabe eben etwas anders aus und muß auch an die Projektion angepasst werden.
3: Na, was denkst Du denn? Wenn sie es sich einfach machen: Pythagoras bei hinreichend kleinen Strecken - andernfalls eine der üblichen Formeln für Geokoordinaten.
4: Wieso sollte man damit etwas vermessen?
Okay, Danke für die Antwort. also senk Umgebungsprespektive, weil das Satellitenbilder sind , schätz ich. Wie heißt das auf englisch?
zu 4) Man gibt gewisse UTM Koordinaten von 2 Punkten an. Das sind kartesische Koordinaten. Beispielsweise E330.000 N5.000.000 und E330.100 N5.000.000
dann haben wir ja eine Differenz von 100m in den Koordinaten, eine Länge in Richtung Osten. Das entspricht, aber nicht in Echt 100Metern auf dem Referenz Ellepsoid des ETRS89. Die Koordinaten sind ja bezogen auf eine flache Fläche und damit geht eine Verzerrung einher. Wenn ich jetzt 2 Punkte ins Gelände bringen will, die Koordinaten ausrechne, habe ich eben in Echt eben nicht einen Abstand von 100m .
Kann Dir leider nicht sagen, wie das Pendant auf Englisch heißt. Im Endeffekt ist das ja weniger ein klassischer Kartennetzentwurf, als die Frage, wie stelle ich einen 3D-Köper (Ellipsoid) am Monitor dar, daß er eben wie ein solcher aussieht.
(Letztlich mache ich doch folgendes, ich habe eine Kugel im 3D-Raum, die hinter der Monitorebene liegt - dann frage ich mich, was der Betrachter vorm Monitor an Position X,Z sieht - Das Ergebnis entspricht hier eben gerade einer 'Aufnahme' über dem gleichen Ursprung in der zum Zoomfaktor passenden Flughöhe)
-----
Wie GE das rechnet kann ich Dir nicht sagen, aber im Endeffekt-> zugehörige Polarkoordinaten bestimmen, dann mit Hilfe des Ellipsoids (Sicher, daß nicht WGS-84 verwendet wird?) die Länge des Bogens bestimmen.
Zum Thema Distanzberechnung bei Geokoordinaten gibt es umfangreiche Literatur und Formelsammlungen - Es ist zwar 'nur' Trigonometrie, aber eben auch nicht total trivial.
Erst recht nicht, wenn DU bedenkst, daß zwischen den Punkten eine Höhendifferenz liegen kann und der Höhenverlauf (an der Oberfläche) nicht linear ist - Da kommst Du dann zwangsläufig zur Frage: Wie genau darf (muß) es denn sein?
Abschließend: Es müßte doch für UTM auch Formeln geben, wie Distanzen im Zuge der Projektion verzerrt (gestreckt) werden. Diese Faktoren kommen dann natürlich in die Berechnung rein.
-------
Hier schon reingeschaut?
Die Textur muss ja nach bestimmten Maßen erstellt werden.
Die Textur wird ja auch größer oder kleiner, wenn ich ran oder raus zoome. Demenstprechend existiert auch ein gewisser Maßstab, der vom User verändert wird, ob der dort irgendwo angegeben wird, weiß ich nicht.