Permutationen in C++?
Ich habe folgenden Code in Python geschrieben, den ich nun aus Performancegründen in C++ schreiben möchte. Ich habe schon einiges probiert, bin aber nicht weitergekommen. Kann mit jemand dabei helfen? Danke schon mal im voraus.
verbotene_paare = [(1, 13), (2, 14), (3, 15), (4, 16), (5, 17), (6, 18), (7, 19), (8, 20), (9, 21), (10, 22), (11, 23), (12, 24)]
for perm in permutations(range(1, 25), 12):
if not any(pair[0] in perm and pair[1] in perm for pair in verbotene_paare):
Ich möchte also alle Permutationen der Zahlen 1 bis 24 mit genau 12 Elementen je Permutation, dabei darf 1 nicht mit 13 auftauchen etc.
2 Antworten
- Und wo in Deinem Code ist der PermutationsAlgoritmus?
- Welchen möchest Du benutzen?
Die Frage ist nur rhetorisch... Ich nehme an Du bist von selbst auf Heaps Algorithmus gestoßen. und gleich die schlechte Nachricht...
Du kannst nicht innerhalb des laufenden Heap-Permutators unerwünschte Ergebnisse entfernen!Egal ob die in meinen folgenden Demos verwendete rekursive Variante (oder iterierend) der jeweils nächste Schritt verwendet das Ergebniss des Vorherigen. Wenn Du eine Kombination nicht weiter verwendest , fällen die daraus folgenden Zweige der Baumstruktur ebenfalls weg.

Das ist auch der Grund weshalb man einen Permutator mich Multithreaded laufen lassen kann aufteilen kann! 🤔 (stimmt nicht so ganz : OuelletHuttunen )
Allerdings kannst Du auch bei dem OuelletHuttunen (Indexed) keine Elemente ausschließen. Es gibt ergo keine Möglichkeit etwas zu entfernen, bevor die Arbeit beendet ist.
...und da komme ich zu Deinem Snipped. Du führst nur die Elemente auf welche ausgeschlossen werden sollen. . Da bleibe ja nicht zum permutieren... Deshalb nehme ich an du hast vor, aus den 24 Einzelelementen alle möglichen Kombinationen zu bilden dabei ist Dir entgangen, das auch C++ dich bei Kombinationen von 24 Elementen nicht retten kann.
24 Elemente ergeben 620448401733239439360000 Kombinationen!
24! = 1*2*3*4*5*6*7*8*9*10*11*12*13*14*15*16*17*18*19*20*21*22*23*24 = 620448401733239439360000
selbst wenn jede Kombination im Speicher Deines Rechner (ohne Verwaltungsinformationen) nur 24 Byte verbraucht, brauchst Du 13868102470038222,65625 GB Speicher!
...mal zum vergleich der Zahlen:
Netto Speichebedarf: 14890761641597746544640000
32GB RAM : 34359738368
2TB SSD : 2199023255552
...aber selbst bei 12 Elementen kommst Du ohne immensen Verwaltungsaufwand weder in Python noch in C++ zurecht mehr als 2GB kann kein normales Array ... https://stackoverflow.com/questions/52427788/allocating-an-array-greater-than-2gb-in-c-or-c . Naaj, der Rechner ist auch nich schnell genug selbst wenn Du C++ vewendest , unter mehreren Tagen geht bei bei 12 Elementen nichts! Bei der Zeitkalkulation von 24! seigt mein Umrechnungsroutine aus.... Soviel Zeit ist noch nicht mal seit dem Urknall vergangen! ein par Milliarden Jahre spielen da keine Rolle-
Es macht also keine relevanten Unteschied was für eine Programmiesprache ich verwende.... Ich setze auf Powershell das ist zwar nicht schnell, aber ich habe noch ein altes Script zum Anpassen rumliegen.
Ich verwende auch keine Zahlen , sondern Buchstaben (Kombinationen), Warum auch ob Buchstaben oder Zahlen ist völlig irrelvant.,
Erstmal ein kleine Demo, wie der Zeichentausch läuft...
Heap-Pemute.ps1
#colordefinition ansicolors definieren
$esc=[char]27
$green="$esc[92m"
$red="$esc[91m"
$resColor="$esc[0m"
$greenPattern='{0}$0{1}'-f $green,$resColor
$redPattern='{0}$0{1}'-f $red,$resColor
#ende colordefinition
function permute ([char[]]$str , $Size ){
if($Size -eq 1){
$str -join ''
}
else{
$LastIndex = $Size-1
$switch = $Size -band 1 -bxor 1 # 1 oder 0 , bitoperatinen sind schneller als Modulo 2
permute $str $LastIndex
foreach ($i in 0..($LastIndex-1) ){
$currendPosition = $i*$switch
Write-Host $( $($str -join '') -replace $str[$LastIndex], $redPattern -replace $str[ $currendPosition], $greenPattern ) '--> ' -n
#tausche elemete
$str[$LastIndex], $str[ $currendPosition] = $str[ $currendPosition], $str[$LastIndex]
Write-Host $( $($str -join '') -replace $str[ $currendPosition], $redPattern -replace $str[$LastIndex], $greenPattern )
permute $str $LastIndex
}
}
}
$myStr = 'abcd'
$permCount=iex($myStr.length..1 -join '*')
$stopwatch = [system.diagnostics.stopwatch]::StartNew()
#start Permutation
$AllPermutations=permute $myStr ($myStr.Length)
$stopwatch.Stop()
"$($stopwatch.Elapsed.TotalMilliseconds) Millisekunden"
Write-Host "$permCount Permutationen moeglich"
Read-Host 'Enter um forzufahren'
$AllPermutations|% {$i=0}{'{0} {1}'-f $_ , (++$i)}
pause

...und wie man ungewünschte Zeichen Kombinationen entfernt
Demo2.ps1
#colordefinition ansicolors definieren
$esc=[char]27
$green="$esc[92m"
$red="$esc[91m"
$resColor="$esc[0m"
$greenPattern='{0}$0{1}'-f $green,$resColor
$redPattern='{0}$0{1}'-f $red,$resColor
#ende colordefinition
function permute ([char[]]$str , $Size ){
if($Size -eq 1){
$str -join ''
} else{
$LastIndex = $Size-1
$switch = $Size -band 1 -bxor 1
permute $str $LastIndex
foreach ($i in 0..($LastIndex-1) ){
$currendPosition = $i*$switch
$str[$LastIndex], $str[ $currendPosition] = $str[ $currendPosition], $str[$LastIndex]
permute $str $LastIndex
} } }
$myStr = 'abcdefgh'
#RegEx für die Buchsabenkombis, welche nicht zulässig sind (🙄statt deiner Zahlenkombinationen)
$SchlechtePattern = 'ab|cd|ef|gh'
$permCount=iex($myStr.length..1 -join '*')
Write-Host "$permCount Permutationen moeglich"
$stopwatch = [system.diagnostics.stopwatch]::StartNew()
$AllPermutations=permute $myStr ($myStr.Length)
$stopwatch.Stop()
"$($stopwatch.Elapsed.TotalMilliseconds) Millisekunden"
"$($AllPermutations.Length) Permutationen gesamt gefunden"
"unzulaessigen Kobinatione: $($SchlechtePattern -replace '\|' , ' , ' )"
Read-Host 'Enter zum Aussortieren der schechten'
#die Schlechten aussortieren
$DieSchlechten = @()
$DieGuten = $AllPermutations|%{$i=0}{
if ($_ -match $SchlechtePattern ) {
#die schlechten ins Kröpfchen,
Write-Host Schlechte Kombination gefunden: $( $_ -replace $SchlechtePattern,$redPattern )
$DieSchlechten += $_
}
else{
#die Guten ins Töpfchen...
$_
}
}
"$($DieSchlechten.Length) Elemente mit unzulaessigen Kobinatione"
"$($DieGuten.Length) zulaessige Elemente"
Read-Host 'Enter um forzufahren'
$DieGuten|% {$i=0}{'{0} {1}'-f $_ , (++$i)}
pause

8 Zeichen = 4 "schlechte" Kombis sind als Anschauung genug.
Überigens, ist der Flaschenhals bei Consolenprogrammen nicht die Operation selbst, sondern Die Anzeige auf dem Bildschirm
Du kannst ja mal 10 Buchstaben /5 Kombis verwenden:
$myStr = 'abcdefghij'
$SchlechtePattern = 'ab|cd|ef|gh|ij'
Die Kalkulation der Permutation (ohne Screenoutput) dauert vielleicht ne halbe Stunde, die Anzeige der "schlechten" Kombinationen will nicht Enden...! (dabei Bedarf der "AusSortier"-Code kaum Leistung)
Auf Rosetta Code findest Du Code für fast jede gängige Sprache...

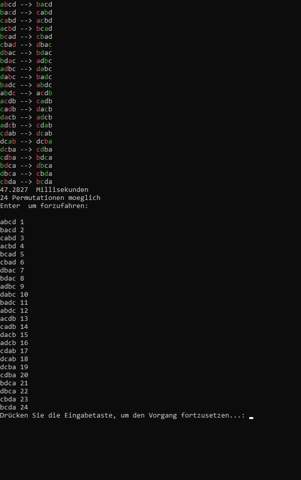

PS:
Man kann innerhalb der Permutations-Funktion die unzulässigen Ergebnisse aussortieren. ...Aber erst, nach dem jeweils der aktuelle "Ast" komplett abgearbeitet ist.
Dies bringt keine Reduzierung der durchzuführenden Permutationen. Es wird lediglich innerhalb der Funktion entschieden, ob das Ergebnis gespeichert wird.
90% der benötigten Zeit entfallen auf die Anzeige... also die "Write-Host"-Zeilen innerhalb der Funktion (im Normalbetrieb) auskommentieren
update.ps1
clear-host
#colordefinition ansicolors definieren
$esc=[char]27
$green="$esc[92m"
$red="$esc[91m"
$resColor="$esc[0m"
$greenPattern='{0}$0{1}'-f $green,$resColor
$redPattern='{0}$0{1}'-f $red,$resColor
#ende colordefinition
function permute ([char[]]$str , $Size ){
if($Size -eq 1){
$result = $str -join ''
#nichts anders als die vorherige Variante...
#bringt keine wesentlich Beschleunigung, da an diesem Punkt
#bereits der gesamte Verzweigungsbaum abgearbeitet wurde
if ($result -notmatch $SchlechtePattern ) {
Write-Host "behalte Ergebnis : $( $result -replace $result,$greenPattern )"
#die Guten ...
return $result
} else {
Write-Host "verwerfe Ergebnis: $( $result -replace $SchlechtePattern,$redPattern )"
}
} else{
$LastIndex = $Size-1
$switch = $Size -band 1 -bxor 1
permute $str $LastIndex
foreach ($i in 0..($LastIndex-1) ){
$currendPosition = $i*$switch
$str[$LastIndex], $str[ $currendPosition] = $str[ $currendPosition], $str[$LastIndex]
permute $str $LastIndex
}
}
}
#Main
$myStr = 'abcdefgh'
$SchlechtePattern = 'ab|cd|ef|gh'
$permCount=iex($myStr.length..1 -join '*')
"unzulaessigen Kombinationen: $($SchlechtePattern -replace '\|' , ' , ' -replace $SchlechtePattern,$redPattern )"
"$permCount Permutationen moeglich"
sleep 3
$stopwatch = [system.diagnostics.stopwatch]::StartNew()
$DieGuten = permute $myStr ($myStr.Length)
$stopwatch.Stop()
"$($stopwatch.Elapsed.TotalMilliseconds) Millisekunden"
"$($DieGuten.Length) zulaessige Elemente gespeichert"
Read-Host 'Enter um anzeigen der ermittelten zulässigen Kombis'
$DieGuten|% {$i=0}{'{0} {1}'-f $_ , (++$i)}
pause
std::array<int, 25> a;
std::iota(a.begin(), a.end(), 0);
do{
for(std::pair<int, int>& forbidden : forbidden_pairs){
bool found_forbidden = false;
for(int i = 0; i < 12; ++i){
if(forbidden.first == a[i]){
if(found_forbidden){
...
}else{
found_forbidden = true;
}
}
}
}
} while(std::next_permutation(a.begin(), a.end()));
Geht evtl. auch effizienter. Das Durchsuchen nach den verbotenen Paaren kann man anders gestalten, evtl. sogar vorab nur Permutationen erzeugen, die diese gar nicht enthalten. Evtl. kann man auch einen passenden Comparator erzeugen oder sonstiges, um das ganze auf die Länge 12 zu optimieren.
Worauf beziehst du dich? Auf das Aussortieren verbotener Paare vor dem Erzeugen der Permutationen?
Folgender Pseudoalgorithmus:
Für alle Zahlenn im Range bilde Kombinationen bestimmter Länge ohne Beachtung der Reihenfolge
Wenn Kombination enthält verbotenes Paar, dann gehe zur nächsten Kombination.
Andernfalls bilde alle Permutationen für die gegebene Kombination.
vor dem Erzeugen der Permutationen?
Genau...
Ich habe mich vor langer Zeit mal eingehend mit der Materie auseinander gesetzt. Es wäre doch eine tolle Sache , wenn man bereits bereits vor Beginn der Permutation ausschließen bestimmte "Pfade" ausschließen könnte . Ich bin dabei natürlich auf die Nase gefallen. Weil's eben (aus oben beschriebenen Gründen) nicht gehen kann. In der nächsten Ebene und denen darunter, verschwindet die unerwünschte Kombinaton (größtenteils) wieder...
Immerhin würde die Pemutation von 24 Elementen (ibei ca 100microSec/tausch) 1,9 Billonen Jahre benötigen. Wenn das vom Fragesteller angedachte Vorgehen möglich wäre, würde die Anzahl der Permutationen auf 1/3 reduziert...
Ob 1,9Billion oder 600Mrd Jahre.... Das macht bei unser Lebensspanne keinen Unterschied....
Übrigens eignet sich Python , Powershell oder Javascript viel besser zum experimentieren, als C++. Und wenn ein Algorithmus mit wenigen Elementen in den ScriptSprachen funktioniert, ist es kein Problem diesen auf eine Compilersprache zu portieren .
Dass der Fragesteller wegen der "Langsamkeit" von Python auf C++ wechseln will, zeigt nur das er die Dimensionen des Themas völlig unterschätzt.
Und so wie in meinem Pseudocode geht es nicht?
Es werden klar nur die Permutationen wegggelassen, die verbotene Paare enthalten und klar alle anderen Permutationen weiterhin erzeugt.
Man schneidet dabei genau die Pfade weg, die man nicht haben will.
Das Erzeugen der Kombinationen ohne Beachtung der Reihenfolge könnte ein Problem sein. Einerseits erzeugt man in jedem Fall jeweils mindestens eine Kombination die die verbotenen Elemente enthält, um die Zweige, die auszusortieren sind zu identifizieren.
Andererseits gilt noch zu beweisen, dass das Erzeugen der Kombinationen ohne Beachtung der Reihenfolge geht ohne alle Permutationen zu Erzeugen.
Wenn ich aber mal davon ausginge, dass die Implementierung in der Python-Dokumentation zumindest theoretisch korrekt ist, so sollte das schneller gehen:
https://docs.python.org/3/library/itertools.html#itertools.combinations
Es sei zudem zu erwähnen, dass sich das Problem ja vom Standard-Permutationsproblem in der Längenlimitierung unterscheidet. Ohne Längenlimitierung würde es zudem auch keinen Sinn machen, Permutationen auszuschließen, die bestimmte Paare enthalten, denn ohne Limitierung enthielte jede Permutation alle Paare.
Danke für die schnelle Antwort, ich bin ein absoluter Anfänger in C++ also schon mal sorry für alles dumme was ich mach. Ich habe folgenden Code mal probiert aber er nimmt nur die Zahlen von 1 bis 12. Kann ich das irgendwie simpel ändern bzw deinen Code da hinzufügen/ersetzen?
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
vector<int> createSubset(int start, int end, int k) {
vector<int> subset;
for (int i = start; i <= end && k > 0; ++i) {
subset.push_back(i);
--k;
}
return subset;
}
int main() {
vector<pair<int, int>> verbotene_paare = {{1, 13}, {2, 14}, {3, 15}, {4, 16}, {5, 17}, {6, 18}, {7, 19}, {8, 20}, {9, 21}, {10, 22}, {11, 23}, {12, 24}};
int z = 1;
vector<int> zahlen = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24};
vector<int> zahlenSubset = createSubset(1, 24, 12);
do {
bool isValid = true;
for (auto pair : verbotene_paare) {
if (find(zahlenSubset.begin(), zahlenSubset.end(), pair.first) != zahlenSubset.end() &&
find(zahlenSubset.begin(), zahlenSubset.end(), pair.second) != zahlenSubset.end()) {
isValid = false;
break;
Du hast keinen Code gepostet der compilen würde. Das erstellen einen Subsets ist auch sinnlos, du nimmsteinfach nur die ersten 12 Zahlen des Arrays.
ok danke für die Antwort. Ich habe noch eine Frage: Wie kann ich alle Permutationen der Zahlen 1 bis 24 (aber nur 12 Elemente je Permutation) generieren?
Da habe ich mir auch schon überlegt, wie das sinnvoll ginge.
Ist nicht ganz einfach, wenn du dafür std-Funktionen verwenden willst. Da müsste man evtl. eine besondere Datenstruktur oder einen besonderen Comparator verwenden.
Ansonsten kannst du aber natürlich auch selbst eine Permutationsfunktion schreiben.
Vielleicht findet sich auch etwas dazu im Internet.
zahlen = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24};
24! Bis zum Ende der Zeit...
selbst wenn jede Permutation nur einen Tick benötigen würde....
Die Python-Implementierung kannst du dir evtl. anschauen:
https://docs.python.org/3/library/itertools.html#itertools.permutations
Das sollte sich in C++ nachimplementieren lassen.
...nö das ist nur Theorie. Wenn man sich nicht mit Permutation beschäftigt hat, sieht die Nummer ganz so trivial aus.
Man kann keinen Ast absägen, ohne die Zweig verdorren zu lassen.
selbst ein Ast, der es auf den ersten Blick "würdig" wäre gekillte zu werden, kann normale "Zweige" haben.