Nullstellen Ableitung?
Stehe gerade merkwürdigerweise total auf dem Schlauch :D wenn eine Funktion f(x) an einer bestimmten Stelle eine Nullstelle hat. was ist dann bei der Ableitung f'(x) an dieser Stelle?
3 Antworten
Damit kliklu mit seiner richtigen Antwort nicht so alleine dasteht :-)
Wenn f´ bei x0 eine Nullstelle hat, dann kann dort eine Extremstelle sein (notwendige Bedingung). Ob x0 tatsächliche eine (relative) Extremstelle ist, muss mit einem weiteren Kriterium überprüft werden.
Deine Frage bezieht sich aber auf Nullstellen von f, nicht auf Nullstellen der Ableitung. Und da kann man eben nicht auf eine irgendwie geartete Eigenschaft der Ableitung schließen. Ich füge mal einen Funktionsgraphen bei. Und da siehst Du: an einer Nullstelle von f kann eine positive Steigung, eine negative Steigung oder auch eine waagerechte Tangente vorliegen. Alles ist möglich.
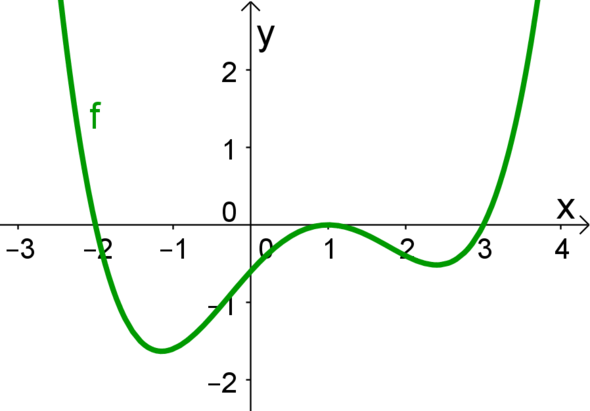
Wenn f(x) eine Nullstelle hat und f '(x) ≠ 0, dann schneidet die Tangente an der Stelle die x-Achse.
Ist f(x) = 0 und f '(x) = 0, dann hat die Kurve eine waagrechte Tangente.
Mann kann es auch umdrehen:
Wenn in einer Nullstelle eine waagrechte Tangente ist,
dann ist f '(x) = 0
(bei anderen waagrechten Tangenten allerdings auch).
Das hängt von der Art der Nullstelle ab, wenn es eine einfache Nullstelle ist, dann kann man nicht sagen, was bei f'(x) ist, bei z.b. einer doppelten hingegen kann man sagen, das auch f'(x) dort wieder eine Nullstelle hat.
Vielen Dank für deine Antwort :) dann bin ich bei meiner Aufgabe jetzt auch überfragt :D