Monotonietabelle aufstellen Sinus cosinus?
Heyyy ich muss bei der Aufgabe eine Monotonietabelle aufstellen jedoch probiere ich mich schon seit einigen Stunden durch und komm noch immer zu keiner Lösung…

1 Antwort
Bestimme die Ableitung.
Untersuche wo die Ableitung positiv ist (dort steigt die ursprüngliche Funktion) und wo die Ableitung negativ ist (dort fällt die ursprüngliche Funktion). Dabei ist es hilfreich zunächst die Nullstellen (und gegebenenfalls Polstellen) der Ableitung herauszufinden, da dort die Ableitung ihr Vorzeichen wechseln kann.
======Bei Teilaufgabe a) beispielsweise...======
Nullstellen der ersten Ableitung berechnen:
Für alle geraden ganzen Zahlen k und alle x ∈ ]k ⋅ π/2; (k+1) ⋅ π/2[ ist sin(2x) > 0.
Für alle ungeraden ganzen Zahlen k und alle x ∈ ]k ⋅ π/2; (k+1) ⋅ π/2[ ist sin(2x) < 0.
Dementsprechend ist f in den Intervallen [k ⋅ π/2; (k+1) ⋅ π/2] mit geraden ganzen Zahlen k streng monoton steigend, und f ist in den Intervallen [k ⋅ π/2; (k+1) ⋅ π/2] mit ungeraden ganzen Zahlen k streng monoton fallend.
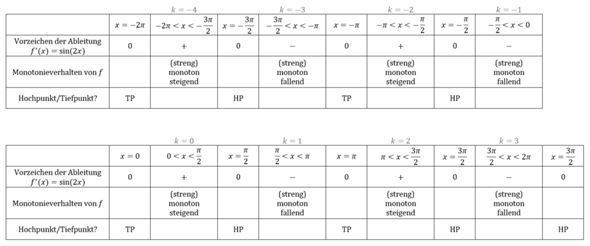
Eingeschränkt auf x ∈ [-2π; 2π] bedeutet das...
======Ergänzung======
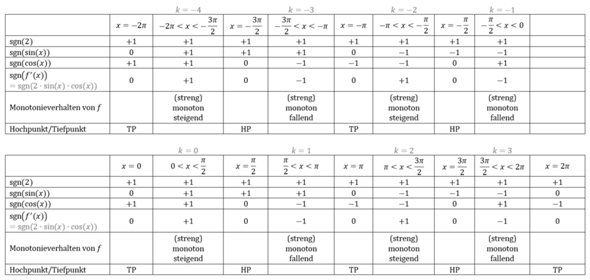
Mögliche Monotonietabelle zu Teilaufgabe a), ohne Ausnutzung, dass 2 ⋅ sin(x) ⋅ cos(x) = sin(2x) ist.
Siehe auch: https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Doppelwinkelfunktionen
sin(2x) = 2 ⋅ sin(x) ⋅ cos(x)
Das ist eine Rechenregel, die ich noch aus meiner Schulzeit kenne. Man kann diese als Spezialfall des Additionstheorems
sin(x + y) = sin(x) ⋅ cos(y) + cos(x) ⋅ sin(y)
für x = y sehen.
============
Man muss das auch nicht unbedingt zu sin(2x) vereinfachen, man kann auch die Nullstellen von cos(x) und von sin(x) betrachten, und dann bedenken, dass das Produkt 2 ⋅ sin(x) ⋅ cos(x) genau dann gleich 0 ist, wenn cos(x) gleich 0 oder sin(x) gleich 0 ist.
Bzw. kann man auch die entsprechenden Vorzeichen von sin(x) bzw. cos(x) in der Tabelle aufführen, um dann auf das Vorzeichen von f'(x) = 2 ⋅ sin(x) ⋅ cos(x) zu schließen.
Heyy ich hätte noch ne kleine Frage, undzwar bildest du ja die Ableitung von (sinx)^2 und das ist ja dann mit der Produktregel 2*sinx*cosx -> Aber nun verstehe ich nicht wie man daraus dann auf sin(2x) kommt. LG und nochmal vielen Dank für deine Hilfe!!!