Mit Reihenfolge vs ohne Reihenfolge?
Guten Tag, ich verstehe nicht ganz warum eine Variation mit Reihenfolge ist und Kombinatorik ohne Reihenfolge. Ich komme immer durcheinander. Bsp. Variation: 1;2;3 und 3;2;1 sind 2 Möglichkeiten, weil mir die Reihenfolge egal ist Kombination: 1;2;3 = 3;2;1 ist eine Möglichkeit, weil die Reihenfolge wichtig ist. Aber dann ist es ja andersrum. Variation heißt man beachtet die Reihenfolge nicht, was ist hier mein Logikfehler?
3 Antworten
Variation: Mit Reihenfolge
Kombination: Ohne Reihenfolge.
Variation: 1;2;3 und 3;2;1 sind 2 Möglichkeiten, weil mir die Reihenfolge egal
Wenn dir die Reihenfolge egal wäre, hättest du nicht gerade zwei Zahlenfolgen mit unterschiedlicher Reihenfolge doppelt gezählt, sondern nur einmal.
Kombination: 1;2;3 = 3;2;1 ist eine Möglichkeit, weil die Reihenfolge wichtig ist.
Genau umgekehrt. Hier ist dir die Reihenfolge egal, also zählst du Zahlenfolgen mit unterschiedlicher Reihenfolge nur einmal.
Warum zählst du dann "1;2;3 und 3;2;1" getrennt? Da du das bei der Variation als zwei getrennte Möglichkeiten betrachtest, nimmst du ja auf die Reihenfolge Rücksicht.
Aber es ist mir doch egal welche Reihenfolge es ist
Das wäre der Fall, wenn ich z.B. 1,2,3 und 1,3,2 als eine Möglichkeit betrachte (Kombination). Die Reihenfolge ist mir egal, daher zähle ich das als eine einzige Möglichkeit.
Ich versteh es einfach nicht, es will nicht in mein Kopf. Kla wenn man es wie du betrachtest achtet man auf die Reihenfolge, aber dann ist es doch relativ wie man an die Aufgabe ran geht und man kann nicht sagen Variation=mit Reihenfolge, sondern Variation = alle Reihenfolgen werden mitgezählt Variation =/ es wird auf die Reihenfolge geachtet. Kann man darin nicht viel zu viel Interpretieren, oder bin ich wirklich einfach gerade überarbeitet und sollte eine Pause machen? xD
Egal ist es nicht (je nach Aufgabe), denn z.B. muss man bei der Anzahl der 4-stelligen Passworter einer Fahrradkette die Reihenfolge beachten (Variation!) und bei der Anzahl der Möglichkeiten, wie man 4 Äpfel auf 2 Teller aufteilen kann, die Reihenfolge nicht beachten (Kombination!)
Im ersteren Fall ist es nämlich wichtig, ob man 1234 oder 1324 eingibt (zwei verschiedene Codes, Reihenfolge wichtig) und im zweiten Fall ist die Reihenfolge unwichtig, denn es ist egal, ob auf dem Teller Nr. 1 Apfel Nr.1 neben Apfel Nr. 2 liegt oder Apfel Nr. 2 neben Apfel Nr. 1 liegt.
Oder anders ausgedrückt:
Reihenfolge beachten: (1,2) nicht dasselbe wie (2,1)
Reihenfolge nicht beachten: (1,2) ist dasselbe wie (2,1)
Aber ja, du hast gerade wahrscheinlich irgendeine Denkblockade. Vielleicht überlegst du dir das später nochmal^^
OK ich ich merk mir es einfach anders, ich habe es mir nämlich so gemerkt:
Variation heißt es werden alle Reihenfolgen mitgezählt (also egal welche Reihenfolge tatsächlich eintritt, es werden alle mitgezählt) Kombination: wdh. Reihenfolgen werden nicht gezählt (man muss also auf die Reihenfolge achten, damit sie nicht wdh. werden)
Ich habe mir einen neuen gebastelt wäre nett, wenn du mich zum Abschluss noch bestätigen könntest und ich diesmal alles richtig interpretiere :D
Variation: Man achtet auf alle Reihenfolgen, man zählt alle mit (deswegen mit Reihenfolge)
Kombination: Wdh. Reihenfolgen werden ignoriert (deswegen ohne Reihenfolge)
"wiederholende Reihenfolgen" ist etwas schwammig, aber ich glaube, du meinst das richtige, also Reihenfolgen mit denselben Zahlen/Objekten?
Wenn ja, dann passt das.
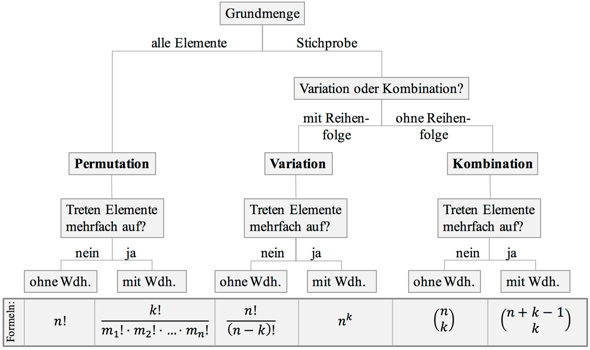
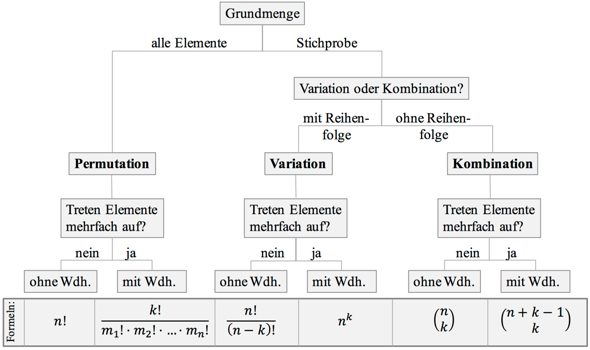
Sieh dir vielleicht auch mal diese Grafik an, die fasst alle Fälle ganz gut zusammen.
Du vermischt hier Reihenfolge wichtig bzw unwichtig und mit und ohne Wiedeholung;
es gibt also 4 Fälle.
https://wissenschafts-thurm.de/grundlagen-der-statistik-kombinatorik-variationen-und-kombinationen/
mal gucken :
Drei verschiedene Kugeln lecker Eis im Becher : Kombination (wenn es egal ist, wo sie in ihm liegen )
Wer aber Wert auf gestapelte drei Kugeln legt : Variationen .
Dann muss n(Kom) < n(Var) sein .......schauen wir mal : 6 Sorten und 3 Kugeln
VAR 6!/(6-3)! = 6*5*4 = 120
KOM (6 über 3) = 6!/(6-3)! * 3! = 20
passt
Variation: Aber es ist mir doch egal welche Reihenfolge es ist. Ich nehme alle Möglichkeiten und achte nicht auf die Reihenfolge. Auf die Bedingung Reihenfolge wird nicht geachtet