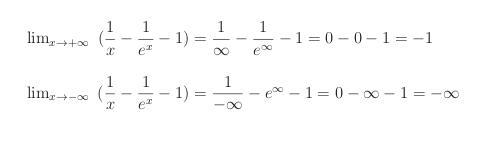Mathearbeit! Woran erkenne ich,ob ein Graph gegen plus oder minus unendlich geht?
Ich schreibe am Mittwoch Mathe und brauche eine kurze Erklärung von irgendjemand.Und zwar weiß ich nicht,woran man erkennt,ob ein Graph gegen plus unendlich oder minus unendlich geht...ich erkenne es einfach nicht.Ich meine allerdings ohne zu zeichnen,sondern nur an der Funktion erkennen.
Ein Beispiel wäre (ihr könnt auch ein anderes Bsp. nehmen,aber das hier ist schön schwer und passt zum Thema e-Funktionen): f(x)=x-exex Jetzt soll ich erkennen,gegen was das für + und - unendlich geht.
Im Lösungsbuch steht: für x⇒ + unendlich geht f(x)⇒ -1
für x⇒ - unendlich geht f(x)⇒ - unendlich
aber WARUM? wie kommt man da drauf?Bitte helft mir,ich habe keinen blassen Schimmer davon... :( (vielleicht könnt irh auch noch ein normales Bsp. ohne e-Funktion nehmen...)
4 Antworten
Falls ihr Maple benutzt kannst du folgendes eintippen:
restart:
limit(solvef(x),x=infinity);
oder
limit(solvef(x),x=-infinity);
Ich hoffe, dass da jetzt kein Tippfehler drin ist. :D Wenn eine Fehlermeldung auftritt, kannst du ja immer noch [Help] benutzen. Viel Erfolg bei der Mathearbeit !
Was genau hat man sich denn unter exex vorzustellen? ich nehme ja nicht an, dass damit e * x * e * x = e² * x² gemeint ist, denn sonst wäre die Lösung des Lösungsbuches ja falsch ^^
Ich nehm einfach mal folgendes (relativ einfaches) Beispiel:
f(x) = x + e^x.
Als erstes lassen wir x⇒ + unendlich laufen. Dann geht logischerweise x⇒+unendlich und e^x⇒+unendlich, also läuft auch f(x)⇒+unendlich (grob kann man sagen, dass unendlich + unendlich = unendlich).
Jetzt lassen wir x⇒ - unendlich gehen. Damit geht x⇒ - unendlich und e^x⇒0. (Das muss man einfach wissen, dass sich e^x für ganz kleine Zahlen der Null annähert.)
Damit geht aber f(x)⇒ - unendlich + 0 = - unendlich.
Nehmen wir ein weiteres Beispiel:
g(x) = x * e^x. Wieder lassen wir x⇒unendlich laufen. Damit geht
g(x) ⇒ unendlich * unendlich = unendlich.
Für x⇒ - unendlich gilt:
g(x) ⇒ - unendlich * 0 = - (0 * unendlich). Mhm, sowas dummes, 0 * unendlich ist gar nicht definiert. Jetzt musst du dich aber daran erinnern, dass die e-Funktion stärker ist als jede Potenzfunktion, also geht sie schneller gegen 0, als x gegen - unendlich geht. Das klingt zwar ein bisschen eigenartig, ist aber so ;) damit bekommt die 0 mehr Gewicht als - unendlich und der Grenzwert von g(x) ist somit 0. (Ich erinnere dich erneut: Das liegt NICHT daran, dass unendlich * 0 = 0 ist! ^^)
Am besten ein letztes Beispiel, ganz ohne e-Funktion:
h(x) = x² * 1/x. Ich weiß natürlich selbst, dass man hier einfach ein x kürzen könnte, aber es soll veranschaulichen, dass unendlich * 0 = 0 im Allgemeinen falsch ist.
Wir lassen wieder x⇒ unendlich laufen. Dann geht x²⇒ + unendlich und 1/x ⇒ 0.
Wieder müsste gelten: h(x) ⇒ unendlich * 0. Aber x² geht schneller gegen unendlich, als 1/x gegen 0 läuft (das liegt daran, dass x² schneller gegen unendlich läuft als x.)
Somit gilt: h(x) ⇒ + unendlich
kannst dir einfach hohe Werte ausrechnen und schauen, was rauskommt. Wenn immer höhere Zahlen rauskommen, geht es wahrscheinlich gegen plus unendlich, wenn immer tiefere Zahlen (Negative Zahlen) herauskommen geht es gegen minus unendlich...
Ausserdem kannst du es auch an der Richtung erkennen, falls die Richtung einheitlich ist...
Bei parabeln geht es z.B. nach dem Zeichen vor x quadrat, nehme ich an...
Hallo sunnykaninchen,
siehe Bild. Einfach + oder - ∞ einsetzen und schauen, was rauskommt. Das Ergebnis muss nur eindeutig sein, eventuell erst ausklammern und kürzen etc.. Wenn ∞/∞ oder 0/0 oder 0/∞ oder ∞/0 rauskommt, dann Regel von L'Hospedale anwenden.
Gruß vom leiermann