Mathe und Idee des funktionalen Zusammenhangs?
Kann mir bitte jemand die Aufgabe erklären, ich verstehe diese Themen fast überhaupt nicht...


3 Antworten
Bei solchen Aufgaben benutzt man im Normalfall die Scheitelpunktform
Wird angewendet,wenn man den Scheitelpunkt direkt ablesen kann
f(x)=a2*(x-xs)²+ys
Scheitelpunkt Ps(xs/ys) mit xs=-(a1)/(2*a2) und ys=-(a1)²/(4*a2)+ao
allgemeine Form der Parabel f(x)=a2*x²+a1*x+ao
quadratische Ergänzung für die Umwandlung der allgemeinen Form in die Scheitelpunktform


Masthöhe bei x=20 m (Ursprung des x-y-Koordinatensystems liegt im Scheitelpunkt)
f(x)=12,5m=a*(20m)²
a=12,5 m/400 m²=0,03125/m
y=f(x)=0,03125*x² also (3)
c) Abstand zwischen den Seilen s=20m/4=5 m
Seil 1 S1=0,03125*(5m)²=0,78125 1.te Seil rechts neben dem Scheitelpunkt
Seil 2 S2=0,03125*(10m)²=3,125 m 2.te Seil rechts neben dem Scheitelpunkt
Seil 3 S3=0,03125*(15m)²=7,03125m 3.te Seil
Seillänge gesamt auf einer Seite Sges=2*(0,78125+3,125+7,03125)=21,875m
d) Die Parabel können wir nach oben verschieben.Die Nullstellen liegen dann auf der x-Achse.
Nullstellen bei x1=-5 m und x2=5m
f(x)=-0,16*x²+c mit c=Höhe h=?
f(5)=0=-0,16*5²+c → c=h=0,16*25=4 m
f(x)=-0,16*x² und der Höhe h=4 m und der Breite des LKW kann man dann die Höhe ausrechnen,wo der LKW durchfährt
Breite des LKW b → f(b)=0,16*b²
Hier Infos,vergrößern und/oder herunterladen


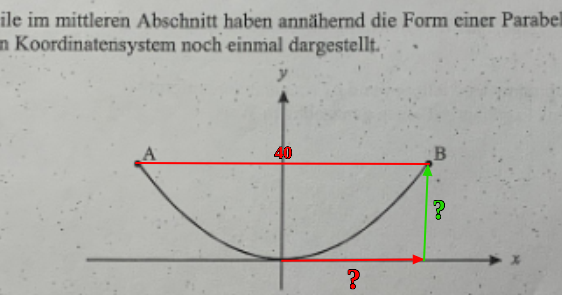
Bei 35a sollst du die Pfeile (für A bitte selbst einzeichnen) beschriften und die Koordinaten von A und B bestimmen.

A und B haben den Abstand 40 m. Sie liegen 12,5 m über der Fahrbahn.
Wie weit liegt A oder B von der y-Achse, entfernt?
Wenn man sich die Zeichnung so ansieht, 20 Einheiten (B).
Die beiden Punkte liegen 12,5m über der Fahrbahn. Die Fahrbahn ist die x-Achse.
Die Höhe ist der y-Wert der Punkte.
Welcher y-Wert liegt 12,5 Einheiten über der Fahrbahn? Der y-Wert der Fahrbahn ist 0.
y = 12,5
Und jetzt mach aus 20 Einheiten in x-Richtung und +12,5 auf der y-Achse zwei Koordinaten.
B (20|12,5), A schaffst du selbst.
ist das für dich nachvollziehbar?