Mathe Stochastik- Glücksrad dreimal drehen?
Hallo!
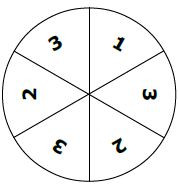
das unten abgebildete Glücksrad stimmt nicht ganz überein. Das Richtige, dass eigentlich für die Aufgabe vorgesehen ist, ist von 1-6 beschriftet. Die wahrscheinlichkeit bleibt gleich.
Aufgabe:''Das abgebildete Glücksrad (siehe unten) wird dreimal nacheinander gedreht. Mit welchem Term kannst u die Wahrscheinlichkeit dafür berechnen, dass mindestens einmal eine 1 oder eine 6 gedreht wird?''
Lösung: 1- (2/3)^3
Meine Frage: WIe kommt man darauf? Ich wollte eigentlich ein Baumdiagramm zeichnen, aber das wäre zu aufwendig gewesen...Gibt es eine andere Möglichkeit?
Ich würde mich echt freuen, wenn mir jemand antworten würde !:) danke schonmal!
2 Antworten
schreibe dir auf in welchen fällen bei 3 maligem drehen die summe 6 am Ende raus kommt. Dann musst du für die einzelnen Ereignisse die Wahrsheinlichkeiten ausrechenn. Das werden viele sein da die Lösung mit einem Gegenereigniss gearbeitet hat, wird wohl die Wahrsheinlichkeit, dass die Summe NICHT 6 beträgt 2/3 hoh 3 sein.
die Wahrscheinlichkeit, dass keine 1 oder 6 gedreht wird liegt pro Drehen bei 2/3 da 3mal gedreht wird ist die Warscheinlichkeit nicht die 1 oder 6 zu drehen (2/3)³ die gegenwahrscheinlichkeit ist dann deine Lösung. Wenn nicht jedes mal keine 1 oder 6 gedreht wurde, wurde mindestens einmal eine 1 oder 6 gedreht.