Mathe Grenzwerte Berechnen Limes ?
Leute könnt ihr mir erklären wie sie auf die Lösung gekommen ist
wir dürfen keine Taschenrechner benutzen wie hat sie also cos und sin ausgerechnet

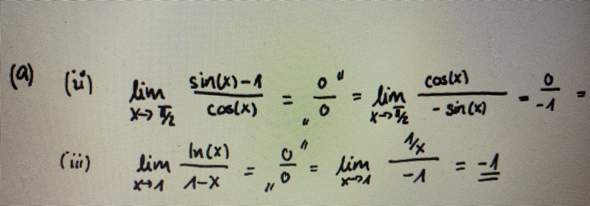
2 Antworten
Leute könnt ihr mir erklären wie sie auf die Lösung gekommen ist
Es wurde die Regel von L'Hospital benutzt.
https://de.wikipedia.org/wiki/Regel_von_de_l%E2%80%99Hospital

===========
wir dürfen keine Taschenrechner benutzen wie hat sie also cos und sin ausgerechnet
cos(π/2) = 0 und sin(π/2) = 1 und ln(1) = 0 sollte man auswendig wissen.
Im Grunde sollte man zumindest die folgenden Werte für sin, cos, tan auswendig wissen...

Bildquelle: https://www.juergen-roth.de/dynageo/trigonom/sin_cos_besondere_werte_loesung.html


Ja, so geht dir Regel von L'Hospital. Einfach die Ableitung vom Zähler und die Ableitung vom Nenner bilden, und dann wieder den Grenzwert bilden. Wenn die Ableitungen an der entsprechenden Stelle stetig sind, kann man einfach die Stelle einsetzen, um den Grenzwert zu erhalten. (Beachte natürlich, dass die Voraussetzungen der Regel von L'Hospital erfüllt sind, also insbesondere, ob man „0/0“ oder „Unendlich/Unendlich“ hat.)
Das sind Werte, die man kennen sollte, wenn man sich mit trigonometrischen Grenzwerten befasst. Schau dir dazu noch einmal an, wo Sinus und Cosinus ihre Nullstellen und Extrema haben.
Ist es beim Regel von l Hospital nicht so das ich einfach eine Ableitung mach und die Werte einsetze ?
so wurde es ja oben gemacht