Mathe Geometrie schnell 🚨?
Hallo ich brauche die Lösung für diese Aufgabe
ich habe alles versucht und ChatGPT kann auch nicht helfen
Geo-gebra classic funktioniert bei mir nicht
kann jemand Foto schicken oder eine Website auflisten wo man das eigeben kann und das es für einen konstruiert?
hier die Aufgabe :
Konstruiere das Viereck mit den Größen
а = 6,5 cm; b = 4,8 cm; с = 5,5 cm; f = 9 cm (Diagonale zwischen B und D), a = 70°
Gehe folgendermaßen vor:
- Zeichne eine Skizze, in der du markierst, welche Größen gegeben sind.
- Entscheide mithilfe der Kongruenzsätze für Dreiecke, wie du das Viereck einteilen kannst, um das Viereck mithilfe der Anwendung der Kongruenzsätze für Dreiecke zu konstruieren.
Konstruiere das Viereck mit den Größen
а = 6,5 ст; b = 4,8 ст; с = 5,5 cm; f = 9 cm (Diagonale zwischen B und D), a = 70°
Gehe folgendermaßen vor:
- Zeichne eine Skizze, in der du markierst, welche Größen gegeben sind.
- Entscheide mithilfe der Kongruenzsätze für Dreiecke, wie du das Viereck einteilen kannst, um das Viereck mithilfe der Anwendung der Kongruenzsätze für Dreiecke zu konstruieren.
Danke im Vorraus brauche Antworten bis morgen um 8:00 Uhr
2 Antworten
Mit den Angaben lassen sich zwei verschiedene Vierecke konstruieren (wobei ich denke, dass die Strecke f, bzw. BD innerhalb des Vierecks sein soll.
Du kannst das Viereck ja erstmal geometrisch mit Lineal und Zirkel konstruieren, damit du eine bessere Vorstellung davon hast, was du berechnen sollst:

Ich weiß ehrlich gesagt nicht, wo dir die Kongruenzsätze für Dreiecke hier weiterhelfen sollen.
Du kannst aber mit dem Sinussatz die fehlenden Winkel im Dreieck ABD berechnen und kriegst dadurch auch die Länge der Seite AD. Damit kannst du dann auch die Fläche vom Dreieck ABD berechnen.
Für BCD kannst du auch die Fläche berechnen oder die Winkel mit dem Kosinussatz.
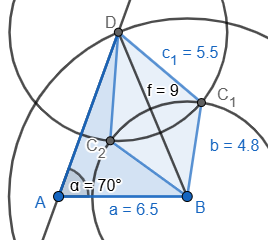
1) Zeichne Seite a = AB = 6,5 cm.
2) Trage in A den Winkel α = 70° ab und verlängere Seite d.
3) Kreisbogen mit Radius f = 9 cm um B. Der Schnittpunkt mit d ist D.
4) Kreisbogen mit Radius b = 4,8 cm um B und Kreisbogen mit Radius c = 5,5 cm um D. Der Schnittpunkt der beiden Kreisbögen ist C.