Mathe - Ableitungsfunktion Tiefpunkt auf X-Achse?
Hallo Leute!
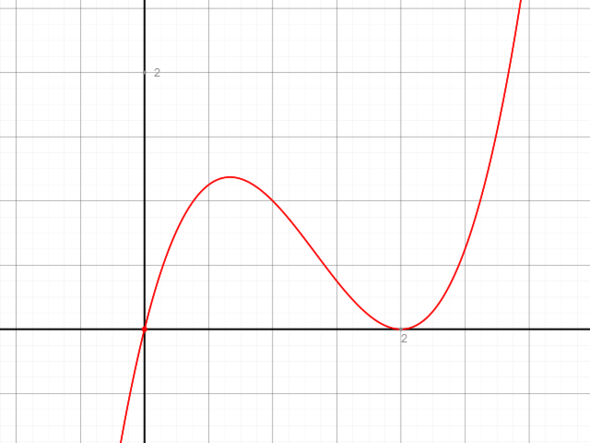
Wir nehmen in Mathe gerade das Thema "Ableitungsfunktionen" durch. Nun haben wir das Schaubild einer Ableitungsfunktion bekommen und müssen die normale Funktion dazu beschreiben. Stellt euch vor, das Bild wäre die Ableitungsfunktion.
Die Ableitungsfunktion hat einen Tiefpunkt (also hat die normale Funktion dort einen Wendepunkt), und der liegt auf der x-Achse (also müsste die normale Funktion dort einen Extrempunkt haben). Das kann die Funktion aber nicht beides gleichzeitig haben o.o
Kann mir jemand erklären, was an dieser Stelle passiert und wo mein Denkfehler liegt?
Danke schonmal im Voraus, LG K8thii ^^
2 Antworten
Wenn die Ableitung an beliebig x = 0 ist heißt es, dass die Steigung der Ausgangsfunktion an der Stelle x, wo die Ableitung = 0 ist ; m = 0 beträgt. An der Ausgangsfunktion ist an dieser Stelle ein Wendepunkt, wo die Steigung 0 ist. Mehr brauchst du darüber gar nicht zu wissen.
Wenn die 1. Ableitung Null ist, dann deutet das auf einen Extrempunkt hin (notwendige Bedingung), aber nur, wenn die 2. Ableitung nicht Null ist (hinreichende Bedingung).
Ein Tiefpunkt im Graphen der Ableitungsfunktion bedeutet ja, dass die 2. Ableitung an dieser Stelle Null ist. In diesem Fall liegt ein Sattelpunkt (quasi ein Wendepunkt mit der Steigung Null) vor.