Kongruenzsätze hilfee?
Hallo. Wie muss ich den Beweis machen?
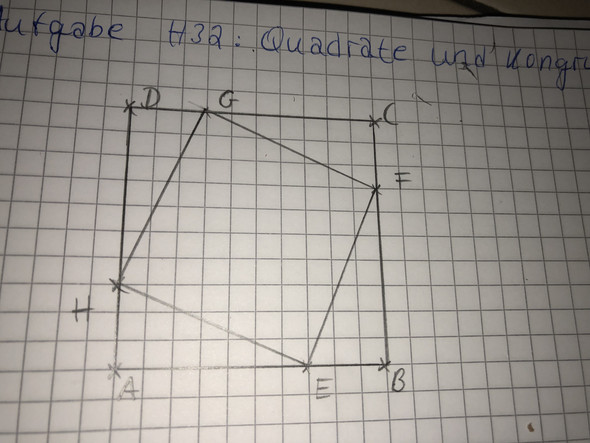
Beweise dass das Viereck EFGH ein Quadrat ist!
4 Antworten
Also das ist letztendlich so was wie der Beweis für den Satz des Pythagoras.
https://de.wikipedia.org/wiki/Satz_des_Pythagoras#Geometrischer_Beweis_durch_Erg%C3%A4nzung
Ich gehe mal davon aus, dass die kürzeren bzw. längeren Teilabschnitte auf dem äußeren Quadrat gleich lang sein sollen.
Wenn der kürzere a und der längere b ist, ist die Hypotenuse der Dreiecke c.
Das äußere Quadrat hat den Flächeninhalt (a+b)².
Zieht man davon die vier Dreiecke mit 2ab Flächeninhalt ab, hat man die Fläche des inneren.
(a+b)²=a²+2ab+b²
abzüglich der 2ab sind das a²+b²=c² (nach Pythagoras).
Also ist das innere ein Quadrat der Seitenlänge c.
Ohne Voraussetzungen kann das alles mögliche sein.
Voraussetzungen:
- die äußere Figur ist ein Quadrat (4 rechte Winkel, gleich lange Seiten)
- die Strecken AE BF CG und DH sind jeweils gleich lang
Dann sind die Dreiecke AEH, BFE, CGF und DHG kongruent (SWS)
Damit ist schon mal gezeigt, dass die Seiten der inneren Figur gleich lang sind.
- Winkel(AHE) = Winkel(BEF) (wg. Kongruenz)
- Winkel(HEA) + Winkel(AHE) + Winkel(EAH) = 180° (W-Summe im 3eck)
- Winkel(HEA) + Winkel(BEF) + Winkel(FEH) = 180° (gestreckter Winkel)
Also ist W(FEH) = W(EAH) = 90°
Mit 4 gleich langen Seiten und mind. einem rechten Winkel handelt es sich um ein Quadrat.
Alternativ kannst du auch einfach zeigen, dass die Winkel in der inneren Figur alle 90° groß sind.
Da die Winkel DHG und AHE zusammen 90° sind, muss der Winkel dazwischen in der inneren Figur ebenfalls 90° sein, da beide zusammen 180° sein müssen.
Naja, wenn du bei nem Viereck mit Seitenlänge c als Flächeninhalt c² rauskriegst, muss es ja ein Quadrat sein. Bei jedem anderen Viereck würde ja ein anderer Flächeninhalt rauskommen. Das hatte ich da als Beweis für angesehen. Aber mit den Winkeln ist es vielleicht eleganter.
Indem du die Winkel misst. Diese sollten alle jeweils 90 Grad betragen. Und die Strecken HE, EF, GF und HG sind alle genau gleich lang. Ich hoffe ich konnte es verständlich rüberbringen. Schönen Abend noch
Ja, so wird's sein. Hauptsache du hast es richtig verstanden. Wie gesagt, "beweisen" hat in Mathe nichts, aber auch gar nichts damit zu tun, dass man etwas abmisst. Das mag vielleicht in der Unter- oder Mittelstufe noch ansatzweise so sein. Aber glaub mir, wenn du sowas in der Oberstufe oder gar an einer Hochschule machst, dann liegst du komplett daneben damit und hast nicht mal ansatzweise die Aufgabenstellung erfüllt.
Du willst es nicht einsehen, oder? Wenn du zwei Vektoren gegeben hast und den Winkel zwischen denen ausrechnen sollst, machst du es dann auch so, dass du die zeichnest und dann den Winkel mit dem Geodreieck misst? Sicherlich ja auch nicht.
Das Problem ist, dass die Aufgabe so wie sie ist schlecht gestellt ist, weil sie der Aufgabensteller vermutlich unvollständig aufgeschrieben und nur die Zeichnung hingemacht hat.
Nicht alternativ sondern ergänzend zu deinem ersten Teil, oder? Es müssen sowohl die Seiten gleich lang als auch die Winkel recht sein.