Köperberechnungen Mathematik?
Könnte mir jemand bei diesen Aufgaben helfen?

Ich bräuchte nur den rechenweg da die lösungen schon hinter den Aufgaben in den Klammern stehen.
Vielen Dank
2 Antworten
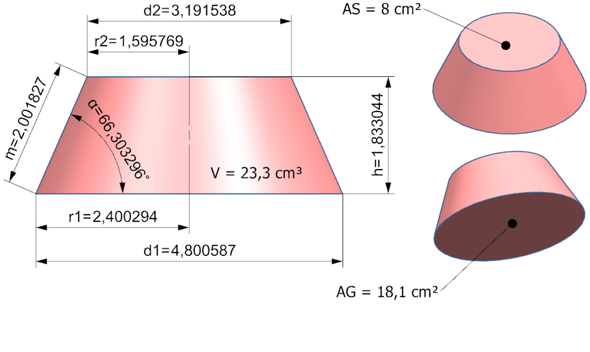
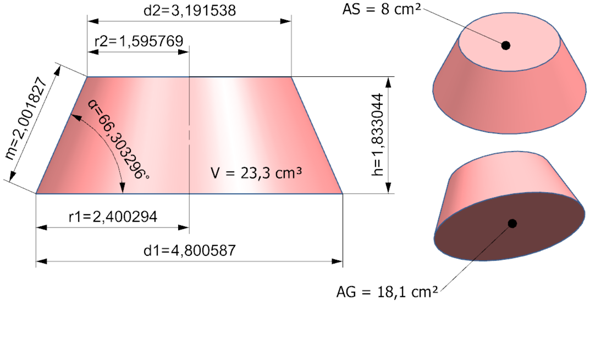
Aufgabe 1
r1 = großer Radius der Grundfläche
r2 = kleine Radius der Deckfläche
AG = Grundfläche
AS = Schnittfläche(Decklfläche)
m = 2 cm
---
AG = r1² * pi
r1 = Wurzel(AG / pi)
---
AS = r2² * pi
r2 = Wurzel(AS / pi)
---
Volumen des Kegelstumpfes würde wie folgt berechnet
V = ((h * pi) / 3) * ( (r1)² + r1 * r2 + (r2)² )
---
Umstellung nach h
h = (V / ((r1)² + r1 * r2 + (r2)²)) * 3 / pi
---
Mantelfläche
AM = (r1 + r2) * pi * m
---
Neigungswinkel
α = Arctan( h / (r1 - r2) )
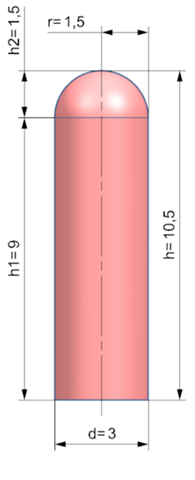
Aufgabe 2
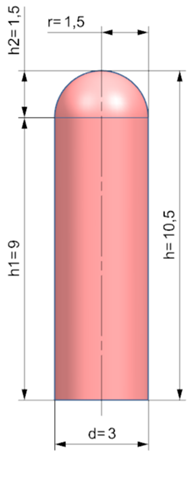
Volumen Halbkugel V1
V1 = (4/3 * pi * r³) / 2
V1 = ((4/3) * pi() * 1,5^3) / 2
V1 = 7,068583 m³
---
Volumen Zylinder V2
V2 = r² * pi * h1
V2 = 1,5^2 * pi() * 9
V2 = 63,617251 m³
---
Volumen Gesamtkörper V
V = V1 + V2
V = 7,068583 + 63,617251
V = 70,685834 cm³
1a)
Deckfläche: π * r² = 8
Grundfläche: π * R² = 18.1
Volumen: h * π/3 * (R² + R*r + r²) = 23.3
r = sqrt(8/π)
R = sqrt(18.1/π)
beide Werte in das Volumen einsetzen:
h * π/3 * (18.1/π+ sqrt(8/π*18.1/π) + 8/π) = 23.3
Daraus folgt h ~ 1.83304 cm
Mantelfäche: M = (R+r)*π*sqrt( (R-r)² + h²)
Werte r,R,h einsetzen: M ~ 25.1309
1b)
(R-r)*tan(α) = h
α = arctan(h/(R-r)) ~ 1.15721 ~ 66.3°
Hinweis: die leicht unterschiedlichen Ergebnisse rühren wahrscheinlich daher, weil man in der Aufgabe mit h = 1.8 gerechnet hat.
2)
Volumen Zylinder: V1 = π * r² * h
Volumen Halbkugel: V2 = 4/6 * π * r³
V1 + V2 ~ 70.6858 m³