Kann mir jemand folgende Trigonometrie-Sachaufgaben lösen bzw. helfen?
Mir ist der Kosinussatz, Sinussatz und der Pythagoras bekannt, jedoch verstehe ich diese Sachaufgabe nicht.
Kann mir jemand helfen, was ich machen muss?
Bitte dringends um Hilfe.
2 Antworten

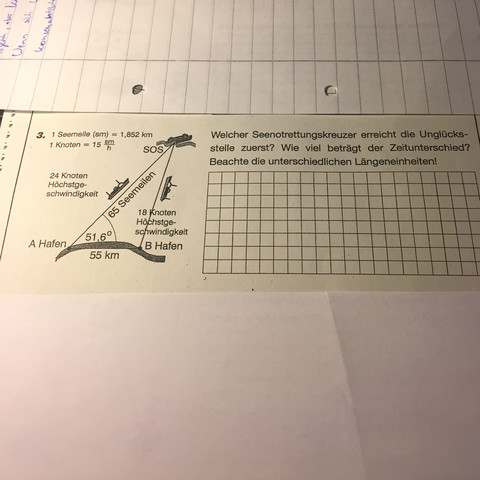
Klingt nach kosinussatz sws 65 Seemeilen, 51,6 Grad Winkel und 55 km... umrechnen der Einheiten, dann die 3 Seite berechnen und anschließend die Zeit für den Transfer berechnen aus weg und Geschwindigkeit

Das linke Rettungsboot kann mit 24 Knoten fahren, dass sind 24*15 = 360 Seemeilen pro Stunde. Die Distanz, die das Boot fahren muss, ist gegeben: 65 Seemeilen. Es braucht also 65/360 = 13/72 Stunden, das sind 10 Minuten 50 Sekunden.
Um herauszufinden, wann das zweite Boot ankommen wird, brauchst du dessen Entfernung zur Unglücksstelle. Die kann über den Kosinussatz ermittelt werden:
Die gesuchte Länge des Dreiecks sei c, die gegebenen 55 km sind b und die 65 Seemeilen = 120,38 km sind a. Der gegebene Winkel ist γ. Dann gilt für c:
c² = a² + b² - 2ab cos(γ)
c² = 120,38² + 65² - 2*120,38*65 cos(51,6°)
c = 94,85
Da das die Distanz in km ist, wandeln wir sie wieder in Seemeilen um: 94,85 km = 51,2149028 Seemeilen
Das zweite Boot fährt mit 18 Knoten = 270 Seemeilen pro Stunde, demnach braucht es für eine Distanz von 51,2149028 Seemeilen genau 51,2149028/270 Stunden = ca. 680 Sekunden, also deutlich länger als das erste Boot.
Das heißt, dass erste Boot wird die Unglücksstelle zuerst erreichen.