Kann mir bitte wer mit einer Aufgabe zu Energieerhaltung helfen?
Ich habe in Physik eine für mich echt schwere Aufgabe bekommen. Könnte mir bitte jemand helfen?
Auf einer Achterbahn bewegt sich ein Wagen (Gesamtmasse 700kg) mit der Geschwindigkeit 3 m/s durch Punkt A und rollt dann antriebslos über B nach C. Der Weg von A nach B beträgt 30m und von B nach C 20cm.
a) Wie groß ist die Geschwindigkeit des Wagens im Punkt C, wenn man von Reibungskraft absieht?
Ich habe da schon Angefangen. E pot (a)+ E Kin (a) = E pot (c) + E kin (c) und E pot= 700 kg * 15m * 9,81= 103005 J. Weiter komme ich nicht
b) Wie groß ist die Geschwindigkeit des Wagens im Punkt C, wenn der Wagen auf der ganzen Strecke von der ganzen Strecke von der konstanten Reibungskräfte 120N gebremst wird?
c) Von A bis B bewege sich der Wagen reibungsfrei. Ab Punkt B werde der Wagen von einer eingebauten Bremse gebremst. Wie groß müsste die als konstant angenommene Bremskraft sein, dass der Wagen genau im Punkt C zum Stehen kommt?
Ich wäre über jede Hilfe und Idee wie ich weiter rechnen soll sehr Dankbar.
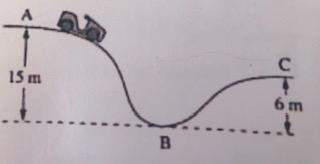
PS: Ich hoffe man kann die kleine Skizze zur Aufgabe sehen
2 Antworten
a) ist richtig und Epot(a) hast du richtig berechnet;
du kannst hier weiter Ekin(a)=0,5mv^2 berechnen und Epot(c) und somit Ekin(c)
entweder stellst du gleich auf vc um oder nachdem du Ekin(c) berechnet hast;
b) die insgesamt Länge von a nach c beträgt dann nach deinen Angaben normal 50m(Denke es ist ein Fehler mit 20cm);
es gilt:
F=m*a; a=F/m
2ax=v^2-vo^2
vo kann man hier als 0 setzen und dann schauen um welchen Betrag sich innerhalb 50m die Geschwindigkeit verringert
dann diese von vc aus a) abziehen
c) hier ist erstmal nicht ganz klar ob von B nach C nur die Bremse wirkt oder auch die Reibung von Aufgabe b) aber ich denke man soll davon ausgehen, dass nur die Bremse entgegenwirkt;
erstmal die vb berechnen, mit dem Ansatz aus a), nur das jetzt auf der Seite wo die Werte mit C waren, jetzt nur Ekin(b) steht;
dann mit:
2ax=v^2-vo^2 wobei vo=vb ist und v=0 ist, da man ja auf 0 abbremsen will; x=20m
auf a umstellen und dann in:
F=m*a einsetzen und F berechnen
2*a*x, a ist die Beschleunigung und x die Strecke( kann man auch mit s bezeichnen);
die Formel ist aus diesen zwei hergeleitet indem man t eliminiert,
x=0,5at^2 +vot
v=vo+at
die Formel 2ax=-vb^2 auf a umstellen und dann a in:
F=ma für das a einsetzen und F berechnen
Noch ein Hinweis:
du kannst die Energie/Arbeit die bei der Abbremsung oder der Reibung aufgebracht wird auch über:
E=Fx berechnen, mit F=Bremskraft oder Reibungskraft und x der Weg;
die Lösung mit E=F*x steht bei der anderen Antwort
also du kannst die Aufgabe hier mit zwei unterschiedliche Ansätze lösen
Erstens:
die Formel ist aus diesen zwei hergeleitet indem man t eliminiert,
x=0,5at^2 +vot
v=vo+at
Jedoch ist mir ein kleiner Fehler bei c) passiert, die richtige Lösung lautet:
man muss zuerst die Differenz von vb-vc bestimmen, da man auch durch die Steigung Bewegungsenergie verliert und diese in Höhenenergie umgewandelt wird;
also gilt dann:
2*a*x=v-(vc-vb)^2 mit v=0, da man ja wissen will welche Bremskraft notwendig ist um auf 0 abzubremsen, also:
a=-(vc-vb)^2 /2*x
und jetzt a=... in:
F=m*a einsetzen, also für a und dann alle Werte einsetzen und F berechnen; die Bremskraft wird hier als negativ definiert...
Noch ein Hinweis: es
du kannst die Energie/Arbeit die bei der Abbremsung oder der Reibung aufgebracht wird auch über:
E=Fx berechnen, mit F=Bremskraft oder Reibungskraft und x der Weg;
die Lösung mit E=F*x sind bei der anderen Antwort jedoch falsch, bei b), da der Energieerhaltungssatz nur ohne Reibung gilt und bei c) ist es nicht ganz richtig, da die die Differenz von E=Ekinb-Ekinc in dem Ansatz verwendet werden muss;
also du kannst die Aufgabe hier mit zwei unterschiedliche Ansätze lösen...
Und nochmal zu b), man kann von der anderen Antwort den Ansatz verwenden nur muss dann Ekinc, das Ekinc von Aufgabe b) sein, was man berechnet, also dann die vc schlussendlich und nicht von Aufgabe a) und Fbrems muss auf der linken Seite der Gleichung abgezogen werden, da die Bremskraft positiv angegeben ist...
Das der Wert negativ ist, ist richtig da die Beschleunigung a oder auch die Kraft in die andere Richtung wirkt wie z.B. die durch die Abfahrt wirkt;
du könntest den Wert auch positiv berechnen oder einfach den Betrag davon nehmen da bei b) in der Angabe die Reibungskraft auch nicht negativ angegeben worden ist
Vielen Dank! Ich habe das jetzt (hoffentlich richtig) eingesetzt bei der b und x=544 raus. Ist das nicht etwas zu viel? Und soll ich es jetzt mit den 106KJ von der c) subtrahieren?
Ah ich habe meinen Fehler verstanden. ich muss auf v^2 bei der B auflösen
b) und c) geht einfacher über den Energieerhaltungssatz.
E pot (a)+ E Kin (a) = E pot (c) + E kin (c) - E Brems
E Brems ist Bremskraft mal Bremsweg.
Aufgabe b)
E Brems = 120N *(30m + 20m) (ich schätze mal, da sollte 20 m stehen und nicht 20 cm)
dann E kin(c) und mit E kin = 0,5 mv^2 die Restgeschwindigkeit berechnen.
Aufgabe c)
Die gesamte kinetische Energie, die in a) herauskommt muss durch das Bremsen in Wärme umgewandelt werden.
E kin(c) = E Brems
E kin(c) = F_Brems * Bremsweg.
F_Brems = E kin(c) /Bremsweg
Vielen Dank! Du hast mir sehr geholfen. Aber ich verstehe die Formel 2ax=v^2-vo^2 nicht ganz was ist 2ax? und wo kommt da die 120 N in der Formel vor?