Ich habe eine Frage bezüglich einer Mathe Aufgabe da ich demnäst eine Prüfung über das Thema habe. Kann mir wer helfen?
Ich habe eine Frage bezüglich einer Mathe Aufgabe die ich für die Prüfung gerade übe und weiß nicht wie ich weiter komme, da ich irgendwas durcheinander bringe. Wir haben gerade Extremalprobleme und da lautet folgende Aufgabe (Bild ist dabei!):
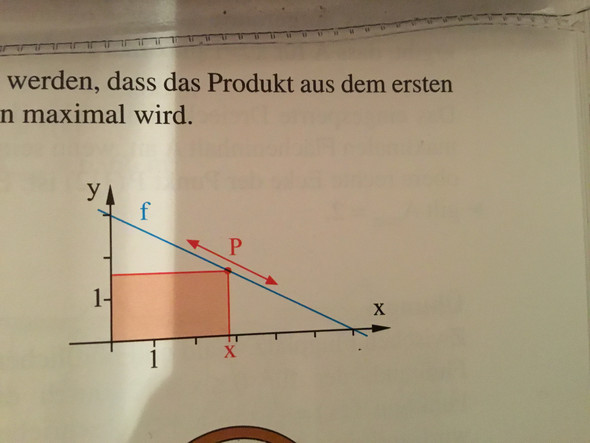
Der Eckpunkt P (x;y) des abgebildeten achsenparallelen Rechtecks liegt auf der Geraden f(x) = 3 - x/2 Wie muss x gewählt werden, damit die Rechtecksfläche maximal wird?
Die Gleichung für die Fläche eines Rechtecks lautet ja A=a*b Und diese soll ja maximal sein. A=> Maximal
Wenn ich jetzt für a, x einsetze und bei b,y dann habe ich in Abhängigkeit:
A(x;y)= x*y
Dazu komm dann die Funktion:
F(x)=y=3-x/2
Wenn ich dann die Zielfunktion bilde, also y mit der Gleichung einsetze sodass nur noch x da ist:
A(x)= x * (3 - x/2) A(x)= 3x - x*x/2
Doch wie rechne ich jetzt die Fläche so aus, sodass sie maximal ist und ich x raus bekomme? Ich selber habe schon gegooglt, aber mir war das alles nichts so einleuchtend sodass ich mir das auch später herleiten kann.
Danke im Vorraus!
2 Antworten
A = -1/2 x² + 3x jetzt mit quadr. Ergänzung die Scheitelform bestimmen.
-1/2 ( x² - 6x) = -1/2 (x-3)² + 4,5
also x=3
Extremwerte ermittelst Du, indem Du die Ableitung der Funktion bildest und gleich Null setzt. Du hast bis hierhin alles korrekt gemacht, jetzt bilde A'(x), setze A'(x)=0 und löse nach x auf.
Der Sinn dabei ist es ja, das Maximum der Flächenfunktion (welche lustigerweise eine Parabel ist) zu finden.
Eine Parabel hat dort den Scheitelpunkt, wo ihre Ableitung eine Nullstelle hat. Dadurch findest du anhand der Ableitungsfunktion die x-Koordinate des Scheitels, die y-Koordinate ist dann die dazugehörige Fläche.
Bei Maximierungs-oder Minimierungsaufgaben geht es (zumindest auf diesem Level) immer um Parabeln und deren Scheitelpunkt.