Kann mir jemand helfen bei der Aufgabe 5a?

2 Antworten
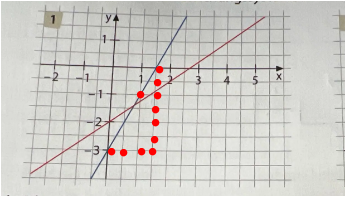
y = mx + b .................b ablesen
m über das Steigungdreieck

3 Einheiten hoch , 1.5 nach rechts : 3/1.5 = 2 ist die Steigung
y = 2x - 3 .....................kontrolle mit x = 1 : y sollte 2*1 - 3 = -1 sein . Passt
.
hat man beide Gleichungen , dann so weiter
( andere Zahlen )
y = 2x - 5
y = 3/4 x - 7
Gleichsetzen : 2x - 5 = 3/4 x - 7
2x - 3/4 x = -7 + 5
5/4 x = - 2
x = -2 * 4/5 = -8/5 = -1.6


Der einfachste weg ist einfach zu jeder gerade eine "normale" Lineare Gleichung aufzustellen und das geht so:
Schritte zur Bestimmung der Funktionsgleichung- Bestimme den y-Achsenabschnitt (b): Lies den Schnittpunkt S(0|b) des Graphen mit der y-Achse ab. Die y-Koordinate dieses Punktes ist der y-Achsenabschnitt b.
- Bestimme die Steigung (m): Wähle einen beliebigen Punkt P(x1|y1) auf dem Graphen.
- Gehe von P aus 1 Einheit nach rechts und dann vertikal bis zum Graphen. Der Abstand nach oben oder unten ist die Steigung m.
Alternativ kannst du die Steigung m aus zwei beliebigen Punkten P(x1|y1) und Q(x2|y2) auf dem Graphen berechnen: m = (y2 - y1) / (x2 - x1).
Setze m und b in die allgemeine Funktionsgleichung f(x) = mx + b ein, um die gesuchte Funktionsgleichung zu erhalten.
Durch Ablesen des y-Achsenabschnitts und der Steigung direkt am Graphen kann man somit die zugehörige lineare Funktionsgleichung bestimmen.
brauche nur die gleichung