Gleichungen mit Summenzeichen umstellen
Ich möchte eine Gleichung wie in dem angehängten Bild nach k umstellen, habe aber leider überhaupt keinen Ansatz wie das gehen könnte. Vielleicht könnte es mir jemand an diesem Beispiel oder auch an einem anderen erklären?
Vielen Dank!
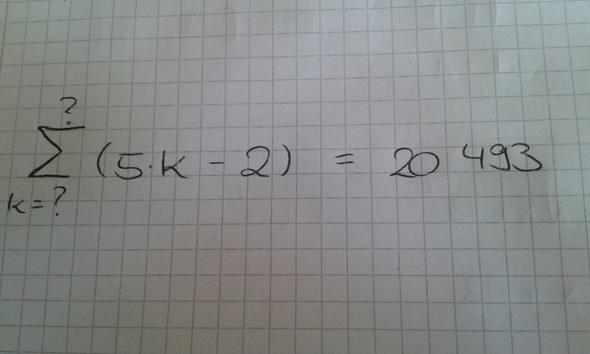
3 Antworten
Ein Versuch einer Antwort (keine Garantie,ob richtig; aberich glaub, sokönnte es gehen):
(k=1; n) Σ(5·k-2)=20493 → k einsetzen →
(5·1-2)+(5·2-2)+(5·3-2)....+(5·n-2) = 20493
-2n + 5·1+5·2+5·3+...+5·n = 20493
-2n + 5·(1+2+3+...+n) = 20493 → Die Summeer Klammer ist (n+1)·n/2 →
-2n + 5·(n+1)·n/2= 20493 → linke Seite vereinfachen und alles auf eine Seite bringen →
5/2·n² + n/2 - 20493=0 → n=90,438 (v -90,638) → Antwort: Wenn du mit k=1 beginnst, musst du bis k=90 (das ist das ? oben auf Σ) einsetzen um die gleichung zu lösen.
Ich hoffe, ich habe keinen Denkfehler begangen, aber es erscheint mir ein richtiger Ansatz zusein :-)
Eine Seite mit k, eine Seite ohne k. Zuerst Klammern lösen: 5×k-2= 20493 dann + 2: 5k=20495 und dann beide seiten durch 5 teilen. k= 4099
Du hast das "Σ"-Zeichen übersehen: dieses bedeutet, dass du für k der Reihe nach 1,2,3,...einsetzen mußt und die Summe aller dieser Terme ist dann 20493. Hättest du nur einen Summanden, dann wäre deine Lösung richtig.
Du kannst überhaupt nicht nach k umstellen, da k eine "gebundene Variable" ist. (Du kannst sie ja "gebunden umbenennen", also z. B. unter dem Summenzeichen und in dem Ausdruck hinter dem Summenzeichen jedes Vorkommen von k durch j ersetzen, ohne dass sich etwas an der Aussage ändert.
Du musst also Summe über k von kMin bis kMax nehmen und diesen Ausdruck ohne Summenzeichen ausdrücken. Das ist glücklicherweise einfach, da es sich um eine arithmetische Reihe handelt. (Formel der Summe siehe dort.)
Da du aber eine Gleichung in zwei Variablen (kMin und kMax) hast, erhältst du arithmetisch eine Schar von Lösungen, aus denen du dann die ganzzahligen heraussuchen musst.
Meine vermutete Antwort dürfte richtig sein → siehe: http://www.wolframalpha.com/input/?i=sum_%28n%3D1%29^m+%285n-2%29%3D20493