Gleichförmige und ungleichförmige Bewegung?
Kann mir jemand den Unterschied zwischen gleichförmiger und ungleichförmiger Bewegung erklären und die zugehörigen Formeln nennen? Weil mit den Formeln hab ich mega Schwierigkeiten. Danke im Vorraus;-)
1 Antwort
Hallo LisJo,
Geschwindigkeit ist eine sogenannte Vektorgröße, eine Größe mit Richtung. Sie wird oft 'v' oder 'v⃑' geschrieben, ich selbst bevorzuge hier '|v›'. Das 'v' kommt vom englischen Wort 'velocity', das diese gerichtete Geschwindigkeit meint - im Unterschied zu 'speed' („Tempo“), das den Betrag ||v›| bezeichnet.
Gleichförmige Bewegung bedeutet, dass |v› zeitlich konstant ist und man die Position |x› (Stell Dir einen Pfeil von einem Bezugspunkt O aus vor) eines Körpers (bzw. seines Schwerpunkts, der Körper als Ganzes ist ja ausgedehnt) durch
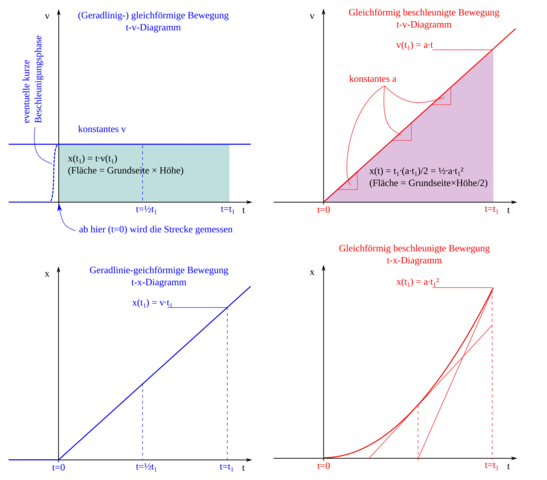
(1.1) |x›(t) = |x›(0) + |v›·t
beschreiben kann. Man spricht zur Präzisierung auch von geradlinig-gleichförmiger Bewegung. Eine solche Bewegung macht ein Körper, auf den keinerlei (resultierende) Kraft wirkt.
Übrigens ist besonders gleichförmige Bewegung relativ: Bewegt sich ein Punkt O' mit |v›, kann ebensogut er als ruhender Bezugspunkt und dafür O als mit -|v› bewegt betrachtet werden.
Dreidimensional ausgeschrieben würde (1.1) etwa
(1.2) (x(t); y(t); z(t)) = (x(0) + v.x·t; y(0) + v.y·t; z(0) + v.z(t))
lauten, wobei das Semikolon für Zeilenwechsel steht. Beschränkt man sich auf eine Richtung und nennt die x, so kann man auch
(2) x(t) = x(0) + v·t
schreiben, wobei v hier als v.x, nicht etwa als Betrag ||v›| aufzufassen ist, d.h., v kann auch negativ sein.
Umgleichförmig heißt eine Bewegung, bei der |v› zeitlich nicht konstant ist, sich also der Betrag, die Richtung oder beides ändert. Im einfachsten Fall gibt es eine konstante Beschleunigung |a›, sodass
(3.1) |v›(t) = |v›(0) + |a›·t
ist. Die einzelnen Komponenten der Geschwindigkeit lassen sich unabhängig voneinander betrachten, etwa
(3.2) (v.x(t); v.y(t); v.z(t)) = (v.x(0); v.y(0); v.z(0)) + (a.x·t; a.y·t; a.z·t),
und für einer Beschleunigung in einer Richtung, etwa x-Richtung mit a=a.x, ergibt sich für die Position
(4) x(t) = x(0) + v(0)·t + ½·a·t²,
denn x ist in einem t-v-Diagramm gleichsam die Fläche unter der Geraden, die v(t) darstellt - präziser zwischen Gerade und t-Achse.
Ein interessantes zweidimensionales Beispiel ist der horiziontale Wurf mit v als Anfangsgescheindigkeit. Wenn wir Luftwiderstand außer Acht lassen können, ist die horizontale Bewegung nahezu (die Erde ist ja eine Kugel) gleichförmig, während der Körper vertikal unabhängig davon frei fällt. Insgesamt ergibt das eine Parabelbahn
(5) (x(t); z(t)) = (x(0) + v·t; z(0) – ½·g·t²).
----
In den Schaubildern habe ich eine 1D-Bewegung mit höchstens konstantem |a› dargestellt.