Gegeben sei ein (nicht überschlagenes) Viereck ABCD mit AB || CD, |AD| = |DC| = |CB| und |DB| = |BA|. Was sind die Innenwinkel dieses Vierecks?
Die andere Frage konnte mir nicht helfen und ich brauche die Antwort heute noch, ich weiß, dass es sich um ein Trapez handelt, bei dem AD, DC und BC gleich lang sind, AB und DC parallel sind und AB dieselbe Länge hat, wie beide Diagonalen. Kann mir wer das genauer erklären, falls das mit dem Kosinussatz gemacht wird, denn davon habe ich keine Ahnung.
3 Antworten
cos α = (AB - CD) / (2 * AD)
α ist der Winkel bei A.
Die anderen ergeben sich von selber.
Der Kosinussatz ist nicht erforderlich, denn man kann auf beiden Seiten ein rechtwinkliges Dreieck konstruieren.
AB - CD ist das Doppelte einer Ankathete von α.
Ich bin zunächst davon ausgegangen, dass die Seitenlängen gegeben sind. Ist das nicht so?
Nein, das sind alle Information, die ich bekomme habe :/
Deswegen ist das ja auch so schwer, wenn man den Kosinussatz noch nicht im Unterricht hatte!
Der Kosinussatz hilft da nicht, denn er braucht für einen Winkel sogar die Längen aller drei Seiten eines Dreiecks. Leider muss ich nochmal weg, werde aber nachdenken und heute Nacht nochmal online kommen.
Vielleicht hat es sogar bis dahin schon jemand endgültig gelöst.
Jedoch möglicherweise sollen die Winkel auch nur in Abhängigkeit von den Seiten ausgerechnet werden. Das werde ich mal versuchen herauszubekommen.
Ich habe meinen Kommentar mit Konstruktionsbeschreibung versehentlich unter die Antwort von @Peter42 geschrieben, wo er gar nicht hingehört. Aber es ist zu spät, um ihn zurückzuholen. Du wirst ihn finden.
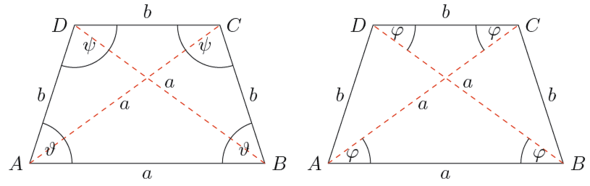
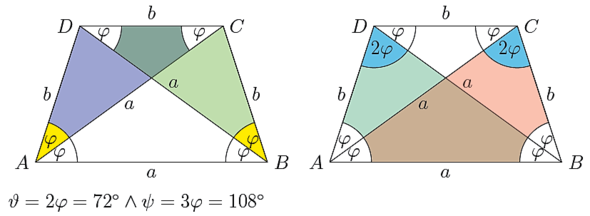
Bestimme die Winkel ∠CAD und ∠CBD, indem du das Trapez in die gleichschenkligen (Winkel an den Schenkeln gleich!) Dreiecke ACD und BCD zerlegst. Danach schaust du dir die gleichschenkligen Dreiecke ABD und ABC an. Am Ende sollte jeder Innenwinkel in Abhängigkeit von φ (oder wie du den Winkel nennen möchtest) angegeben sein. Du zählst alle Winkel eines Dreiecks zusammen und setzt es mit 180° gleich (oder alle Winkel des Trapezes mit 360° gleichsetzen). Wenn du φ hast, kannst du die anderen Winkel berechnen.
Ok, das hört sich wahrscheinlich zeimlich dumm an aber...
Was ist φ?? Und wie soll ich die Winkel CAD und CBD bestimmen, nur mithilfe des gleichschenkligen Dreiecks?
φ ist der griechische Buchstabe Phi. Du kannst den Winkel nennen, wie du willst, wobei man in der Regel Buchstaben des griechischen Alphabets nimmt, z. B. α, β, γ. Wenn du ein gleichschenkliges Dreieck hast, sind die Winkel an den Schenkeln und der Grundseite gleichgroß. ∠DCA ist an einem Schenkel mit Länge b und der Grundseite des Dreiecks ACD, ∠CAD ebenfalls. Damit sind die beiden Winkel gleichgroß.
Je zwei mal 60 Grad und 120 Grad. Die 60 Grad sind am Punkt A und C.
Ich brauche aber einen Lösungsweg. Wie hast du denn herausgefunden?
"Parallelogramm mit allen Seiten gleich lang" war gegeben bzw. hast du selber schon rausgefunden. Der zusätzliche Knackpunkt liegt in der Angabe
/DB/ =/BA/
Das bedeutet nämlich, das ABD ein gleichseitiges Dreieck ist (Dreieck Summe Innenwinkel = 180 Grad = 3x60 Grad).
Und da jedes Viereck die Summe der Innenwinkel = 360 Grad hat, bleibt für die anderen nur 120 Grad übrig.
ABD ist doch kein gleichseitiges Dreieck?? Nur die Seiten DB und BA sind gleich lang, aber AD nicht.
na ok, war ich vielleicht doch ein bisschen zu flott mit meinem Ansatz. Ich denke mal drüber nach...
Die Lösung von @GiftigerOsaft erscheint mir plausibel, obwohl ich sie noch nicht im Einzelnen nachvollzogen habe. (Aber er zeigt die gleichen Winkel auf. Siehe unten!)
Weiterhin kann ich sagen, dass sich die lange Seite des Trapezes zu einer der kürzeren jeweils verhält wie 8 : 5 = 1,6
Allerdings kann ich nicht genau sagen, warum.
Die Konstruktion ist leicht:
a = AB hinlegen, dann Kreisbögen um A und B mit Radius a.
Sodann b = 5/8 * a ausrechnen und wiederum Kreisbögen um A und B. Die Schnittpunkte mit den vorherigen Kreisbögen sind die Punkte D und C.
ABCD verbinden. Trapez ist fertig.
Alle solche Trapeze sind ähnlich und haben die Winkel α = 72° bei A und B an a
sowie 180° - α = 108° bei C und D.
Der Winkel von 72° ist nicht nur abgelesen, sondern mit dem Kosinus aus meiner Antwort verifiziert.
Zum Verhältnis von a und b: Man betrachte beispielsweise das Dreieck ACD mit den Längen b, b und a, wobei der Seite mit Länge a der Winkel 108° gegenüberliegt. Kosinussatz: a = √(2b² - 2b² cos 108°) = √(b²(2 - 2 cos 108°)) = b√(2 - 2 cos 108°) ≈ 1,618b.
Aber wie komme ich auf die Längen? Bzw. wie komme ich bei der Antwort auf eine reelle Zahl?