f(x)=x³+ax²?

Ich brauche dringend Hilfe bei meinen Mathe HA :(

Ich hab schon viele Wege versucht, jedoch komm ich nicht auf die richtige Lösung.

Die Aufgabe lautet: Berechnen Sie a so, dass der Graph einer Funktion f mit f(x)=x³+ax² bei xE=-2 einen Extrempunkt hat.

Vielleicht kann mir da jemand helfen

Danke im Voraus :)

Answer 1

[Hamburger02]

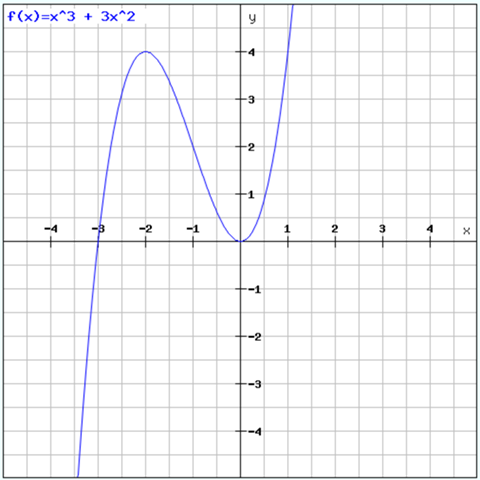
f(x)=x³+ax²

f'(x) = 3x^2 + 2ax

f'(-2) = 0 = 3 * 4 - 4a
4a = 12
a = 3

Damit lautet die Funktion:
f(x) = x^3 + 3x2

Comments

[Xuser2020]

Dankeschön

Answer 2

[gauss58]

Erste Ableitung bilden, diese gleich Null setzen, für x = -2 einsetzen und a bestimmen.

Comments

[Xuser2020]

Könntest du das bitte vorrechnen, bei mir kommt nur Müll bei raus :(

[gauss58]

@Xuser2020

a = 3, Rechnung siehe Hamburger02

[Xuser2020]

@gauss58

Danke

Answer 3

[MagicalGrill]

1. Extremstellen allgemein berechnen (in Abhängigkeit von a).
2. Jetzt ein a berechnen, bei dem eine dieser Extremstellen -2 ist.