Funktionsterm variieren?
Ihr sollt mir jetzt nicht die Aufgabe lösen oder so aber wenigstens erklären wie das geht weil ich es nicht verstehe

1 Antwort
Hi :)
Du musst halt gucken, wie du das ersetzen kannst. Nehmen wir mal a)
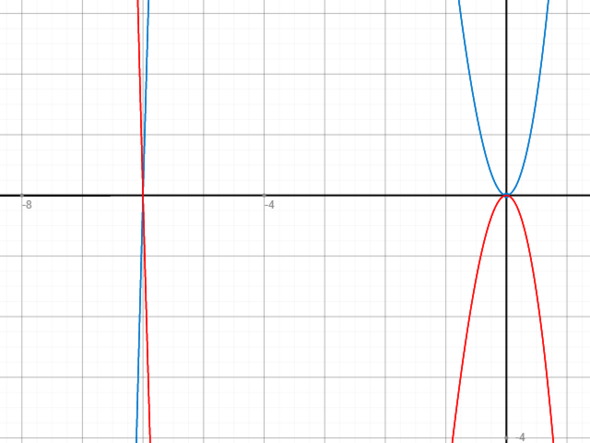
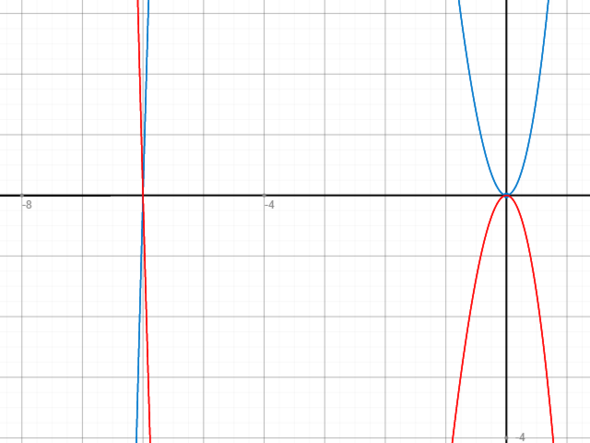
f(x) = 6x² + x³
Wenn du da jetzt große x einsetzt, wird der Funktionswert immer und immer größer - im positiven Bereich!
nun müssen wir den Term so abändern, dass genau das Umgekehrte passiert. Dazu gibt es hiern einen Trick: Wir multiplizieren den Funktionsterm mit -1. Dann wird die Funktion nämlich einfach an der x-Achse gespiegelt ;)
Wäre hier:
g(x) = -f(x) = -6x² -x³
Dann trifft auch definitiv unser Kriterium zu, welches hier gefordert ist :)
Bei b) mach aus x³ einfach x^4 und ändere noch das Vorzeichen des ersten Terms! ;)
Dann hast du 'ne achsensymmetrische Funktion. Sie kommt aus dem Positiven und "verschwindet" wieder in das unendlich Positive, somit ist für beliebig große x-Werte im positiven und negativen Bereich eben x gegen Unendlich.
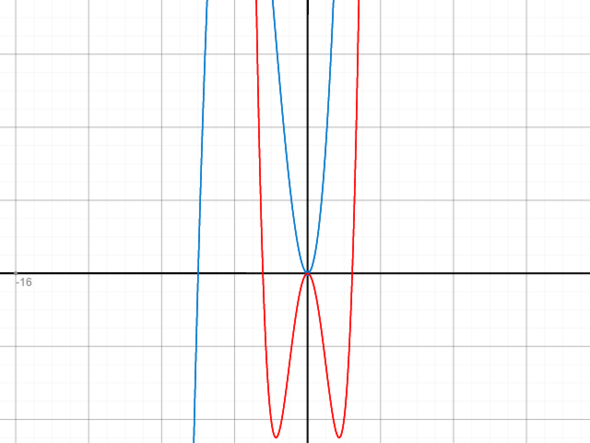
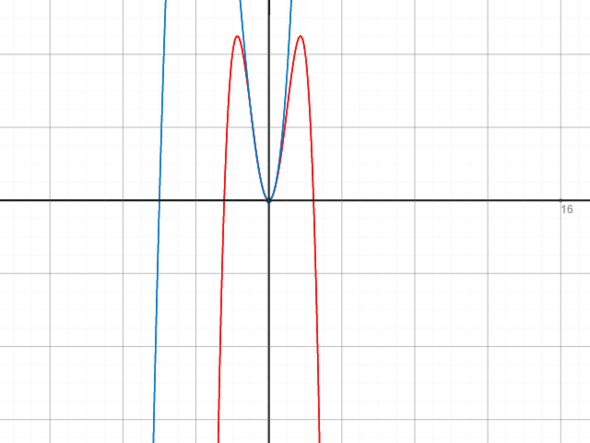
Also hätten wir h(x) = x^4 - 6x²
Jetzt spiegeln wir h(x) wieder an der x-Achse, wir erhalten also
i(x) = -x^4 +6x²
Die Aufgaben d und e sind schon wesentlich kniffliger.
Bei d und e könnte man mit Stauchen und Verschiebung arbeiten. Das musst du aber selbst probieren ;)
Unten mal die Anhänge. Das sind immer die eigentliche Funktiojn (blau) und die neuen Funktionen
LG ShD
Kannst du bei meiner anderen frage auch helfen du bist gut in Mathe da musst du nur gucken ob ich es richtig gemacht habe oder nicht
Was sind das für Bilder ? Ist das schon die Lösung für d und e ?
lies meine Antwort noch einmal gründlich. Ich habe es genau genug erklärt denke ich...
x^4, dass heißt doch so wie x hoch 4 oder nicht?