Fakultät = Exponent Gleichung
Wie kann man eine Gleichung wie die folgende lösen : 2x! = 365^x, in der Fakultät als auch ein Exponent vorkommt Mfg Michi
4 Antworten
Eine von vielen Möglichkeiten (neben der Bisektion) ist die Erzeugung einer selbstkonvergierenden
Iterationsformel - also die Umstellung nach x und Neueinsetzen des berechneten Wertes:
2 * x! = 365^x | log
log(2 * x!) = x * log(365)
x = log(2 * x!)/log(365)
Zum immer wieder Einsetzen (Iteration) eignet sich der Iterationsrechner:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#log(Fak(x) * 2)/log(365)@N@B0]=0.1;@N@Bi+1]=Fx(@Bi]);@Ni%3E14@N0@N0@N#
(LINK endet mit # und beinhaltet den kompletten Algorithmus)
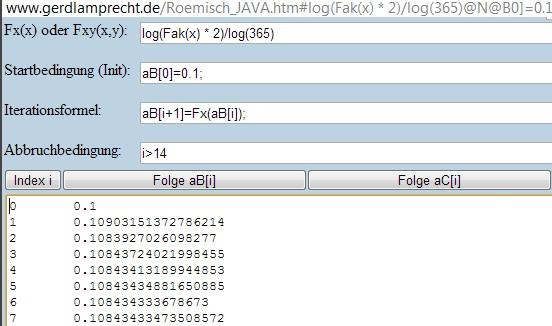
nach über 11 Iterationen hat man schon mindestens 14 richtige Nachkommastellen.
siehe Bild
Interessant: etwas oberhalb von -12 gibt es eine Weitere Lösung, aber da braucht man über 25 Stellen Genauigkeit!
Melde Dich, wenn Du mehr Nachkommastellen brauchst...
Etwas schneller konvertiert die Newton-Iteration:
x=x-(2x! - 365^x)/[2 * Gamma(1+x) * Digamma(1+x)-365^x log(365)]
x=0.10843433466617... (selbe Ergebnis)
(die negativen Lösungen lasse ich mal weg)
Und dann noch eine Lösung um x=987.1003...
(dann ist die Stirling-Formel etwa 3 Nachkommastellen genau, aber das sind Zahlen mit 2530 Stellen vor dem Komma!!)
Achtung: Einige Mathe Lehrer wollen die Gammafunktion-Lösung nicht haben und pochen stur auf "Fakultät nur ganzzahlig" -> dann Lösung von Roach5, also der Beweis, dass es wegen Primfaktoren keine ganzzahlige Lösung gibt.
Das hier ist wohl die vernünftigste Lösung für dieses Problem, wobei man auch kein exaktes Ergebnis bekommt (mir ist auch nicht bekannt, dass man analytisch ein exaktes Ergebnis für solche Gleichungen bekommen kann, das ist aber nur so dahingestellt).
Ich denke außer der Gammafunktion kannst du das analytisch nicht Lösen, du kannst aber Zahlentheorie verwenden, um die UNMÖGLICHKEIT der Gleichung zu beweisen.
365 hat die Primfaktoren 5 und 73, ebenso alle ihre Potenzen.
Wenn wir bei x nur für ganze Zahlen ausgehen (was Sinn macht, da die Fakultät nur für sie definiert ist), können wir sagen, dass 2x! auch die Primfaktoren 5 und 73 haben muss. Da stoßen wir schon auf den Kopf, da der Vorfaktor 2 auch eine Primzahl ist, und diese offensichtlich von 5 und 73 verschieden ist. Das gleiche gilt für die Primfaktoren jedes einzelnen Faktors der Fakultät (2, 3, 4[2 * 2], 5 ist vorhanden, 6 [2 * 3], 7 usw.). Da 2x! und 365^x unterschiedliche Primfaktoren haben, können sie nicht gleich sein. Damit wäre dein Problem gelöst.
Naja, er hat nach der Fakultät gefragt, da hat ers ;)
Man kann weiter beweisen, dass es eine Nicht-ganzzahlige Lösung geben MUSS, da ab x = 366 die Fakultät stärker steigt als die Exponentialfunktion, was vorher nicht der Fall war, damit haben wir hier eine untere Grenze für eine der zwei Lösungen (wenn man negative Werte auslässt), was mit deiner Lösung von etwa 900 übereinstimmt.
P.S.: Ich bin kein Mathelehrer, musste mich mit diesen aber lange rumschlagen ;)
Um ehrlich zu sein kenne ich da kein Verfahren, das direkt zum Ziel führt. Wir haben ähnliches einmal in Physik bei der Herleitung der Orbitalgleichungen lösen müssen, das war damals nicht so einfach ;) (war allerdings in der VL, d.h. es war keine Übungsaufgabe).
Die Berechnung wurde damals vom Prof auch nicht besonders genau ausgeführt.
Numerische Verfahren führen hier aber sicher zum Ziel. Du kannst z.B. f(x) folgendermassen definieren:
f(x) := 2x! - 365^x
und jetzt löst du f(x) = 0 mit dem Newton-Verfahren oder alternativen Verfahren zur Nullstellensuche auf (Sekantenverfahren u.a.).
Ah ja schlussendlich hilft vielleicht noch diese Näherung, mit der du wirklich per Hand eine Lösung bestimmen kannst (ist allerdings auch nicht so einfach!):
x! ~ (x/e)^x sqrt(2 * pi * x) (Stirling-Formel)
Analytisch wüsste ich auch nichts.
Numerisch kannst du die Gamma-Funktion verwenden. ( Γ(x) = (x-1)! )
Ja, der 2. Teil könnte durchaus die Lösung für einen Mathe-Lehrer sein, der die Gammafunktion-Lösung nicht haben will und stur auf "Fakultät nur ganzzahlig" pocht.