Epsilon-Delta Kriterium o.O DRINGEND BITTE EINFACH ERKLÄRT! Mathe Hausaufgabe
Hallo Leute ich bin rel. neu hier und hab gleich mal ein Problem :/
Ich bin im 2ten Semester und studiere einen technischen Studiengang und komm momentan bei EINEM einzigen Thema nicht weiter was ich aber für meine Hausaufgabe brauch, die muss ich nämlich abgeben weil sie benotet wird -.-'
Es geht um das Epsilon-Delta Kriterium und ich werde einfach nicht daraus schlau ! Bin echt verzweifelt hab best. 5 bücher daheim liegen bei 2 wirds sch***e erklärt und in den anderen wirds garnicht erwähnt :/
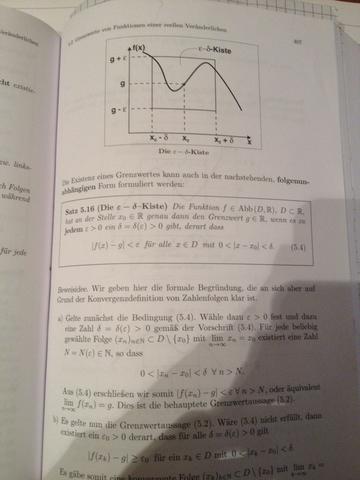
Was ist das E.-D.-Krierium und was diese e-d-Kiste? WOZU brauch ich das und wie wendet man sowas an?! hab auch ein bild aus meinem Lehrbuch mal reingestellt ich hoffe so sehr das mir jemand helfen kann....
Vielen Dank schonmal
1 Antwort
Hi,
ich versuchs mal ganz einfach zu erklären :)
Das Epsilon-Delta Kriterium ist ein Kriterium für Stetigkeit einer Funktion. Und zwar an einer einzigen Stelle x (d.h. dieses Kriterium sagt dir nicht, ob die Funktion als ganzes stetig ist, sondern nur, ob sie an einer stelle Stetig ist).
Stetigkeit bedeutet einfach, dass die Funktion nie springt, d.h. man sie mit einem Stift zeichnen kann, ohne jemals absetzen zu müssen.
Das Epsilon-Delta Kritierium bedeutet jetzt, dass die Funktion an der stelle x stetig ist, falls:
Für alle Epsilon > 0 existiert ein Delta, sodass im Falle von |x-x'| < delta auch |f(x)-f(x')| <epsilon.
Lass dir das einmal ein paar mal durch den Kopf gehen und versuchs zu verstehen, man muss es öfters durchlesen evtl.
Jetzt zur Erklärung: Das Kriterium bedeutet, dass folgendes gilt: Falls die Punkte x und x' ganz nahe beieinander sind, dann sind auch die Funktionswerte nahe beieinander. Stell dir vor, du willst jetzt nachweisen, dass die Funktion an der Stelle x nicht springt. Wenn wir jetzt einen Sprung hätten, z.B. ist die Funktion bis inkl. x noch konstant 3 (als Beispiel) und springt dann sofort nach x auf 4 rauf. Dann wäre das Kriterium nie erfüllt. Denn: Die Funktionswerte x und x' (falls x' etwas grösser wie x ist) können noch so nahe beieinander liegen, der Funktionswert bei x' ist dennoch immer 4 und der bei x immer noch 3.
Falls du noch fragen hast, schreib mir eine Freundschaftsanfrage oder antworte auf meine Antwort. Bin die nächsten paar Stunden noch wach und ich antworte dir (falls die Hausübung bis morgen abzugeben ist).