Ein medizinischer test wird durch eine vierfeldertafel beschrieben?
Aufgabe:
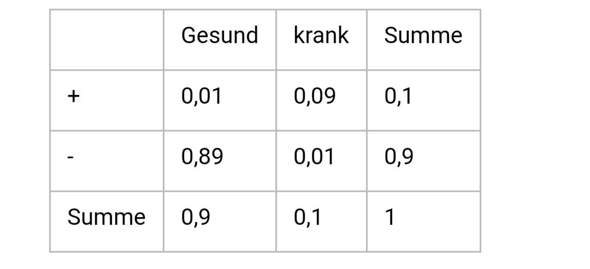
Ein medizinischer test wird durch eine vierfeldertafel beschrieben.
a) Durch welche Zahlen werden a priori- und totale Wahrscheinlichkeiten beschrieben?
b) Mit welcher a posteriori-Wahrscheinlichkeit ist eine Person, bei der der Test ein positives Ergebnis hatte, tatsächlich krank?
c) Mit welcher a posteriori-Wahrscheinlichkeit ist eine Person, bei der der Test ein negatives Ergebnis hatte, tatsächlich gesund?
d) Skizzieren Sie zur Situation b) und je ein verkürztes Baumdiagramm.
Es geht um des satz von bayes. Was ich nicht so recht verstehe. Ich habe versucht es zu lösen bin aber nach langer Überlegung gescheitert. Kann mir bitte jemand helfen :) danke im Voraus
1 Antwort
Die a priori- und totalen Wahrscheinlichkeiten sind die Summen am Ende der Zeilen bzw. Spalten, d. h. z. B. P(+)=0,1; P(Gesund)=0,9.
Die "inneren" Zellen sind die Wahrscheinlichkeiten dafür, dass beides eintritt, also z. B. P(+ und Gesund)=0,01 (im Baumdiagramm sind das die Wahrscheinlichkeiten für den jeweiligen kompletten Pfad).
Die bedingte (a posteriori)-Wahrscheinlichkeit P(A|B) [Wahrscheinlichkeit von A unter der Bedingung, dass B schon eingetroffen ist] errechnet sich so:
P(A|B)=P(A und B)/P(B)
statt P(A|B) schreibt man auch P_B(A) [P mit tiefergestelltem B. kleine Eselsbrücke (so habe ich mir damals gemerkt, wodurch man teilen muss...): das B steht tiefer, also durch P(B) teilen]
(Hast Du z. B. ein Baumdiagramm mit B im ersten Schritt und A im zweiten Schritt gezeichnet, dann ist P(A|B) die Wahrscheinlichkeit des Astes von B nach A.)
b) hier ist bekannt, dass der Test positiv ist, d. h. gefragt ist nach der Wahrscheinlichkeit "krank, unter der Bedingung Test positiv", also:
P(krank|+)=P(krank und +)/P(+)=0,09/0,1=0,9=90%
c) P(gesund|-)=P(gesund und -)/P(-)=0,89/0,9=0,9888...=98,89%
d) für b) zeichnest Du erst den Ast P(+) und dahinter den Ast "nach krank". Der erste Ast P(+) hat ja die Wahrscheinlichkeit 0,1 (hinten die Zeilensumme der Vierfeldertafel). Der gesamte Pfad hat die Wahrscheinlichkeit P(+ und krank), also die entsprechende Zelle (=0,09). Der Ast von + nach krank ist die bedingte Wahrscheinlichkeit P(krank|+).