Baumdiagramm - Wahrscheinlichkeitssberechnung
Hilfe, morgen ist M-Jahrgangsstufen test & ich habe keine ahnung was ein Baumdiagramm ist, folgendes Beispiel war letztes Jahr:
Simon schießt mit seinem fußball auf eine torwand. Zielt er dabei auf das obere Loch, so trifft er dieses mit einer Wahrscheinlichkeit von 20 %, zielt er auf das untere trifft er mit einer Wahrscheinlichkeit von 50 %. Simon schießt zuerst einmal auf das obere und dann einmal auf das untere Loch. Zeichnen sie das dazugehörige, vollständig beschriftete Baumdiagramm und berechnen Sie die Wahrscheinlichkeit dafür, dass Simon mit genau einem der beidern schüsse sein ziel trifft.
Wer kennt sich da aus oder kanns mir erklären?
1 Antwort
Normalerweise werden Baumdiagramme nicht mit Prozentzahlen beschriftet, sondern mit Brüchen. So lassen sich am Ende die Wahrscheinlichkeiten besser ausrechnen. Deshalb rechnen wir erst mal kurz um.
Statt 20% - also 20 von Hundert - kann man auch 20/100 schreiben. Gekürzt: 1/5
Sowohl 20% als auch 1/5 bezeichnen also eine gleichgroße Wahrscheinlichkeit.
50% sind demnach 50/100, also 1/2.
Wie hoch die Wahrscheinlichkeit ist, dass Simon keines der beiden Löcher trifft, wird nicht direkt gesagt, lässt sich aber leicht berechnen. Wir wissen ja, dass er zu 20% das obere Loch trifft und zu 50% das untere Loch. Die Wahrscheinlichkeit, dass der Ball in keins der Löcher geht, beträgt demnach 30%, denn:
100% - 50% - 20% = 30%
Und statt 30%, also 30/100, kann man auch 3/10 schreiben.
So, das erst mal dazu. Weiter geht's.
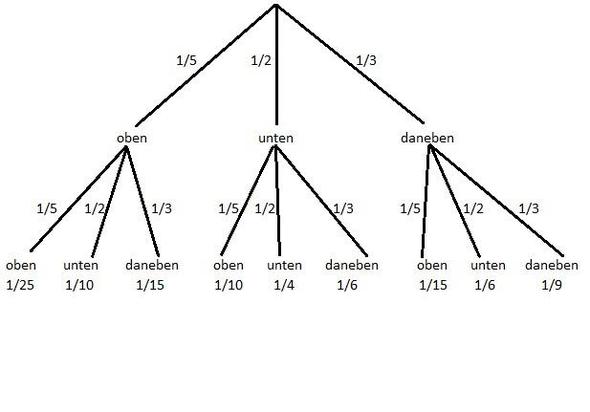
Unten siehst du das zu der Aufgabe passende Baumdiagramm. Erst mal sieht man, dass die einzelnen Wahrscheinlichkeiten an den jeweiligen Äste stehen. Darüber hinaus wird deutlich, dass es um zwei Schüsse geht, da wir sozusagen zwei Ebenen haben. Ginge es in der Aufgabe um vier Schüsse, hätten wir vier Ebenen. Das Prinzip sollte deutlich werden.
Wir wissen also, wie hoch die Trefferwahrscheinlichkeiten bei einem Schuss sind. Um die Wahrscheinlichkeiten der einzelnen Ergebnisse bei zwei aufeinanderfolgenden Schüssen herauszufinden, müssen wir die einzelnen Brüche miteinander multiplizieren, und zwar wie folgt:
Schauen wir uns mal an, wie hoch die Wahrscheinlichkeit ist, dass Simon den Ball zweimal im oberen Loch versenkt. Dass die Wahrscheinlichkeit bei einem Schuss 1/5 beträgt, ist bekannt. Bei zwei Treffern liegt sie bei 1/25. Warum? Die einzelnen Wahrscheinlichkeiten werden miteinander multipliziert, also rechnet man 1/5 * 1/5.
Um das zu verdeutlichen, widmen wir uns mal der eigentlichen Aufgabe. Zwar gibt es vier Wege, bei denen nur einer von zwei Bällen reingeht, aber man muss beachten, dass es um Simons Ziel und um eine Reihenfolge (erst oben, dann unten) geht. Für diese Aufgabe sind also die folgenden zwei Wege interessant:
- Erster Ball geht oben rein, zweiter Ball daneben
- Erster Ball geht daneben, zweiter Ball geht unten rein
Für diese zwei Wege muss nun jeweils die Wahrscheinlichkeit ausgerechnet werden. Für den ersten Fall rechnet man also 1/5 * 1/3 und erhält 1/15. Anhand des Baumdiagramms sollte man diesen Schritt gut nachvollziehen können.
Hat man die Wahrscheinlichkeit beider Fälle berechnet, muss man die Ergebnisse noch zusammenzählen, also:
1/15 + 1/6
= 2/30 + 5/30
= 7/30
Die Wahrscheinlichkeit, dass Simon mit genau einem der beiden Schüsse sein Ziel trifft, liegt also bei 7/30 bzw. ungefähr bei 23%.
dankeschön, hat mir echt geholfen!!!! (: