Beweis, zwei Strecken sind gleich lang?
hallo, es geht um folgende Knobelaufgabe.
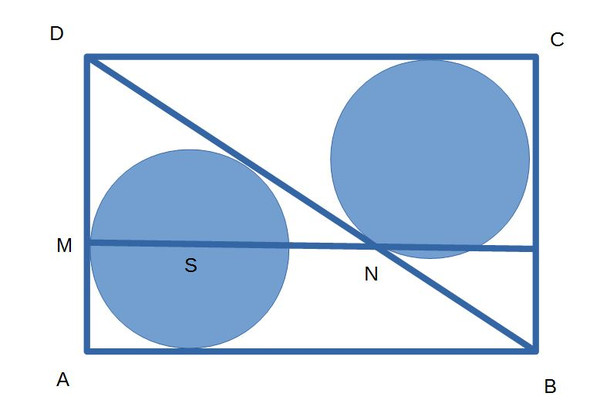
Man soll beweisen, dass die Strecken AD und MN gleich lang sind. MN geht durch den Mittelpunkt des einen Kreises und trifft den anderen an der Tangente.
Habe einige Ansätze versucht: Strahlensätze, über Inkreismittelpunkt (Winkelhalbierende), Cosinussatz etc. Bekomme es aber nicht raus.
Hab Ihr Tipps für mich? Muss nicht direkt eine Lösung sein. Danke und LG
5 Antworten
An die, die es nicht glauben wollen: die Seiten sind gleichlang.
Ich nehme an, SN || AB (sonst gilt der Satz nicht) und stelle fest:
- SN hat von AB den Abstand r (Radius des Kreises).
- Sei S' der Mittelpunkt des anderen Kreises und N' dessen Berührpunkt an BD. S'N' || CD, ebenfalls mit Abstand r.
- T liege auf CD senkrecht über N'. Es gilt |N'T|=r.
Jetzt kannst Du zeigen:
- ∆NSN' ≅ ∆DN'T, also |SN|=|DN'|
- ∆DSN' ≅ ∆DSM, also |DN'|=|DM|
Den Rest überlasse ich dem Leser als Übungsaufgabe :-)
Hallo,
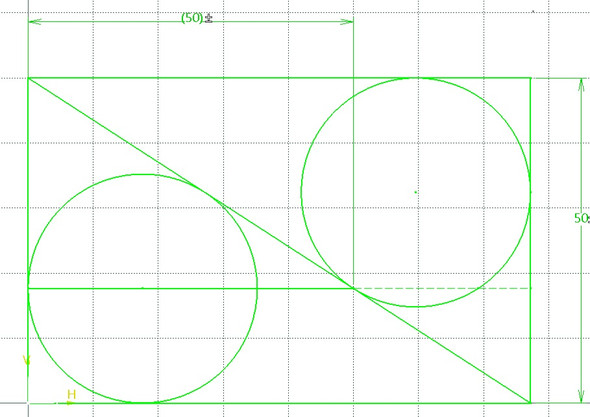
mit Hilfe einer Konstruktion habe ich herausgefunden, daß AD=MN, nicht MD=MN
Auf dieser Grundlage mußt Du weitermachen.
Ich sehe: inzwischen wurde die Frage korrigiert.
Herzliche Grüße,
Willy
Könnte es sein, dass die Frage heißt:
Unter welchen Umständen sind MN und MD gleich lang ?
Weil alleine mit dem Bild ergibt sich ja schon ,dass dem nicht so ist
Oder gibt es noch Vorgaben zu den Streckenverhältnissen die Du unterschlagen hast ?
mein Fehler: man soll zeigen, dass AD und MN gleich lang sind!
Da das Dreieck MND in dieser Abbildung nicht gleichseitig ist, können MN und MD auch nicht gleich lang sein.
MN und MD wären gleich lang für den Fall, dass ABCD ein Quadrat wäre.
Sorry. Das Dreieck muss nur gleichschenklig sein und bei M den rechten Winkel haben.