Bestimmen Sie eine ganzrationale Funktion 3. Grades , deren ..?
Ich komme bei der 5b nicht weiter, kann mir jemand erklären wie ich fortfahren muss und mit welchen Punkten?
hätte f(2)=2
f(3|9)
und W(1|1)
aber ich komme wenn ich diese Punkte in die ganzrationale Funktion einsetze nicht weiter ..

1 Antwort
Eine ganzrationale Funktion3. Grades hat die Grundgleichung
f(x) = ax³ + bx² + cx + d
Du hast also vier Unbekannte: a, b, c und d.
Du brauchst also auch vier Bedingungen. Du hast nur drei aufgelistet. Deswegen kommst du auch nicht auf ein Ergebnis, wenn du nur mit drei Gleichungen rechnest. Dann hängen Ergebnisse z.T. immer noch von Unbekannten ab (dann hast du sowas wie a=3b). Dir fehlt noch eine Bedingung, die du in eine Gleichung bringen kannst.
Die letzte Bedingung kannst du aus dem Wendepunkt zusammen mit dem letzten Satz ziehen. Denk dran: Ein Wendepunkt hat die extremste Steigung. zwischen zwei Extrempunkten. Ausnahme: Sattelpunkte. Genau dieser liegt hier vor, weil dort steht, dass dort die Steigung 0 vorliegt. Ein Sattelpunkt ist ein spezieller Wendepunkt, für den genau diese zusätzliche Bedingung gilt, dass dort auch die Steigung 0 ist. Das hast du normalerweise nie in einem Wendepunkt.
Hier siehst du es perfekt im Vergleich:


Quelle: Mathebibel:

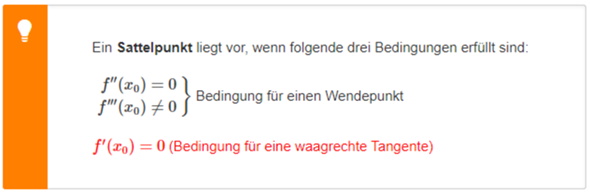
Richtig. Aber auch f'(1) = 0. Du hast also sogar mehr Bedingungen hier, als du brauchst.
Heißt dieser Punkt wäre dann f‘‘(1)=0?