Berechnung von Matheaufgabe (Trigonometrie)?
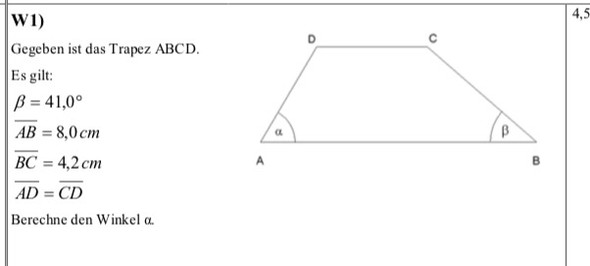
Guten Abend, als Vorbereitung auf die kommende Mathe Prüfung habe ich einige Übungen gemacht. Unter anderem auch im Bereich Trigonometrie. Allerdings bin ich auf eine Aufgabe gestoßen bei der ich einfach nicht weiter komm. Kann mir bitte jemand weiter helfen? Danke schon mal im Voraus :)
3 Antworten
Hallo,
mein Vorschlag:
Zeichne die Diagonale AC ein.
Nach dem Kosinussatz gilt dann:
(AC)²=8²+4,2²-2*8*4,2*cos (41)=5,56 cm (gerundet).
Da die Seiten AB und CD parallel laufen, sind die Winkel BAC und ACD Wechselwinkel und damit gleich groß.
Den Winkel BAC berechnest Du, da nun die Strecke AC bekannt ist, nach dem Sinussatz.
Es gilt:
sin (BAC)/4,2=sin (41)/5,56
sin (BAC)=sin (41)*4,2/5,56=0,49558
Dieser Sinus entspricht einem Winkel von 29,7°
Da AD=DC, hat auch der Winkel CAD 29,7°, ebenso Winkel BAC.
Winkel Alpha gleich >CAD+>BAC=29,7*2=59,4°
Herzliche Grüße,
Willy
Bei solchen Aufgaben immer eine Skizze mit den entsprechenden Hilfslinien machen.
Ergebnis anhand einer Konstruktion überprüft.
Höhe links und rechts einzeichnen; kleinse Stück rechts auf AB nennen wir p
und links q
sin ß = h/BC und h berechnen;
cos ß = p/BC und p berechnen
im linken Teildreieck Pythagoras
h² = AD² - q²
und
8 = AD + q + p weil AD=BC
Unbekannte sind q und AD
mit Einsetzugsverfahren AD und q berechnen;
dann
sin alpha = h/AD
usw
Also: Um eine Lösung zu bekommen kannst du ja schon mal die einfachste aller Möglichkeiten wählen. Zeichen! Du hast ja schließlich die Strecke AB und BC, sowie den dazwischen liegenden Winkel ß (beta) gegeben. Außerdem weißt du, dass AD=BC ist. So kannst du dir schonmal ein Bild davon machen.
Zweite Möglichkeit: https://rechneronline.de/pi/trapez.php
Habs einfach mal gemacht. Kam bei mir für alpha auch 41° raus.
Übernehme aber keine Garantie auf Richtigkeit!
Hoffe ich konnte dir weiterhelfen. Ansonsten einfach mal den Lehrer fragen, ob es nochmal erklären kann. Fragen kostet nichts