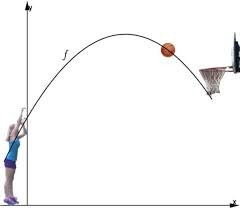
Wie wiet ist die Entfehrung?
für einen Freiwurf beim Basketball wurde für die Höhe y( in m) in Abhängigkeit von der Entfernung x ( in m) vom Abwurf fesgestell
P( 0 | 2) B(0,5 | 2,75) c (1 |3,20)
die Gleicung lautet
f(x)= -0,6x^2+1,8x+2 der Graph ist auch hier .
https://www.mathe-fa.de/de#res
die erste Frage was gemeint genau mit diesem Satz : (für einen Freiwurf beim Basketball wurde für die Höhe y( in m) in Abhängigkeit von der Entfernung x ( in m) vom Abwurf fesgestellt ?)
zweite Frage
wi rechent man die Entfernung anhand der Garph , also von Null oder insgesamt?
Danke
6 Antworten
Also ist die Funktion im Buch bereits gegeben? Musstest du die nicht selbst berechnen? Mit der Funktion f(x)=-0,27x^2+1,5x+2 bekommst du natürlich auch andere Nullstellen.
In diesem Bild ist die grüne Kurve aus den Punkten A,B,C berechnet die gelbe Kurve aus A,B,G. Die rote Kurve ist die, die anscheinend in deinem Buch steht. Da liegen die gegebenen Punkte ganz knapp daneben.


Was ist denn das Thema im Buch? Anscheinend will man hier die Berechnung einer Regressionsparabel sehen. Das macht man aber normalerweise nicht in der schule. Welches Lehrbuch hast du denn da?
9 klasse elemnt der mathmatik rehienland-pfalz
es ist mathe 9 klasse aber ab und zu git er aufgabe, hier sthet ober IM BILDPUNKT
parebel im sport- quadratische regresssion? was ist regression, möchte gern lernen
Schade, dass du dein Handy nicht dabei hast. Ich würde gerne die Seite sehen. Als Schüler der 9. Klasse hat man (meiner Meinung nach) noch gar nicht das notwendige Werkzeug, um eine solche Funktion so exakt wie möglich zu bestimmen.
Meine Idee wäre:
- Alle Punkte zeichnen
- sehen, dass das wie eine nach unten geöffnte Parabel aussieht
- den Scheitelpunkt bestimmen (abschätzen)
- der Abwurfpunkt (0|2) ist gegeben
- Mit dem Scheitelpunkt und einem weiteren Punkt kann man die Funktion bestimmen.
Eine Regression versucht, bei in der realen Welt gemessenen Werten einen Zusammenhang zu finden. Da die Messungen immer etwas ungenau sind, benutzt man Verfahren, die trotz solcher Ungenauigkeiten ein möglichst gutes Ergebnis liefern. Wie du gesehen hast, wird das Ergebnis ganz anders, wenn man sich nur auf die ersten 3 Punkte verlässt.
ich habe dir die Frage gestickt, kann aber ischer morge u+oder über morgen schicken, aber ich abe wie im Buch dir abgescgrieben, aber ich schicke dir spaäter
ich bin baer kein schuler , ich lerne allein,
wie kannst du bestimme , die Joordinate wo der Ball den Kor trifft?
Hier geht inzwischen alles durcheinander, ich muss auch langsam frühstücken ;-)
Zum Lernen: Ja, ich weiß dass du allein lernst (bzw. mit GuteFrage). Aber ein Schulbuch für die 9. Klasse kann ja eigentlich nur das voraussetzen, was ein Schüler in dieser Stufe weiß. Daher hätte mich die genaue Formulierung der Aufgabe interessiert. Moderne Grafische Taschenrechner haben oft Funktionen zur Regression schon eingebaut. Dann muss man nur die Werte eingeben und die fertige Funktion kommt raus. Das ist dann aber keine Mathematik, sondern Tastendrücken. Angeblich hat man dann mehr Spielraum für die Modellierung. Tatsächlich sind es aber immer noch die gleichen Aufgaben wie vor 30 Jahren.
Zum Korb: Du brauchst die Koordinaten des Korbs K(x|y). Dann setzt du x in die Funktion ein und guckst ob f(x)=y. Wenn die Abweichung sehr klein ist (wenige Zentimeter), ist es ein Treffer.
So ich bin jetzt erstmal für ein paar Stunden raus ...
bitte ich werde sehr gern bitte taschenrechner kaufen ,ich schaffe das aber welche soll ich kaufen kannst dmir emphelen, es bitte viele in amazon. du hast aber auch Geduld, das ist doch schön, mach es in ruher später. und guten Apettit
hier ist der Graph, beduetet dieser Satz (((für einen Freiwurf beim Basketball wurde für die Höhe y( in m) in Abhängigkeit von der Entfernung x ( in m) vom Abwurf fesgestellt ?) freiwurf , bedeutet also dass man vor dem Basket steht ,als in bestimmer Enternung, beispeil 5 meter , das nennt man Freiwurf, richitg?
und der Abstand von , wo der Mann mit dem basketkorb , nennt man also diese Enfernung(x) , x ist die Entfernung vom won man steht( Abwurfort) bis zum Basketball.Es ist nicht einfach , das auszudrücken, wollte aber wissen ob ich richtig verstanden haben,
Danke
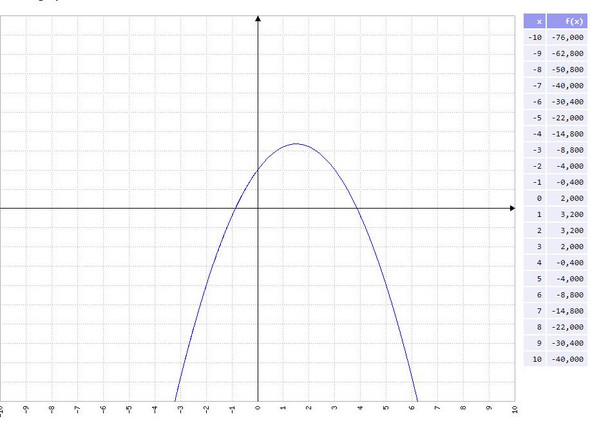

hier ist noch genauer Graph, kannst du mir sagen bitte wo trifft dsen Abll den Basket
also wo waäre die Koordinaten punkt?
ich denke es ist so, dass ich zuerst weissen muss wie wie weit sthet der Werfwer von Basketkor( Aburfort) beusoeil 5 meter, dann sete ich x=5 in der gleichung dann kommt raus y. und dise x und y beiden geben die korrdinaten für den Basketkor( wo de rBall in korb reingeht) ist das richig?
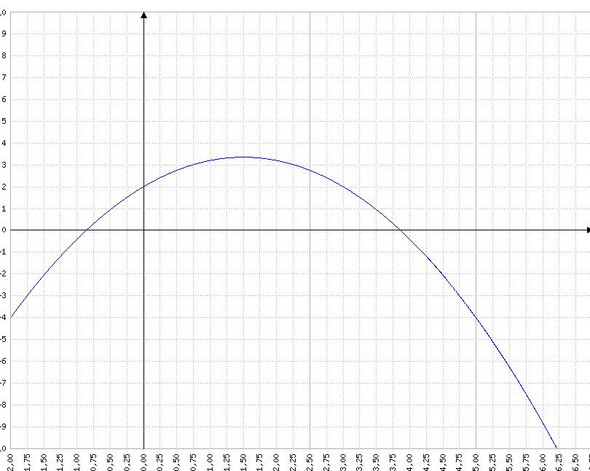

ich denke es ist so, dass ich zuerst weissen muss wie wie weit der Werfwer von Basketkorb steht ( Abwurfort) beispeil 5 Meter, dann setze ich x=5 in der Gleichung dann kommt raus y beispiel 2,5 und dise x und y beiden geben die korrdinaten für den Basketkor( wo der Ball in den korb reingeht) ist das richig?
Wenn der Korb bei x=5 steht, musst du auch noch wissen, in welcher Höher er aufgehängt ist. Laut Basketballregeln ist die Höhe 3,05m. Wenn der Trefferpunkt also (5|3,05) ist und dieser Punkt auf der Wurfbahn f(x) liegt, dann ist es ein Treffer. Dabei bin ich jetzt von einem glatten Durchgang ausgegangen, der Ball kann ja auch am Brett abprallen und dann indirekt durch den Korb gehen.
Wenn der Werfer aber 5m vor dem Korb steht und der Ball schon bei 3,86m landet, kann es kein Treffer sein.
ehlrich bevor ich dich überhauptverstehen kann? wie lautet die Lösung , also die Gleichung?
ist meine Gleichung richitig erstma
y= -0,6x^2+1,8x+2l
WEIL im Buch ander Lösung steht?
die lösung im Buch lautety= -0,27x^2+1,5x+2
also ist richig?
Siehe dazu meine neue Antwort mit Bild. Deine Berechnung aus den ersten drei Punkten ist richtig. Aber anscheinend war das gar nicht verlangt.
Die Entfernung vom Werfer ist auf der x-Achse, die Höhe des Balls auf der y-Achse. Da hat man zwei Punkte auf der Flugbahn gemessen und den Abwurfpunkt bei (0|2),
Mit diesen 3 Punkten kann man eine Parabelgleichung aufstellen. Dann kann man für jede Entfernung vom Werfer die Höhe des Balls berechnen. Wenn die Bahn durch den Korb geht, wird es ein Treffer. Ansonsten landet der Ball bei der rechten Nullstelle auf dem Boden.

ok noch interssante farge, ich sehe jetzt es ist logisch, also die entfernung jetzt fängt bei x= 0 y =2, ok
dann bis der Ball den Korb trifft, aber wo trifft der ball den Basket? wo wäre das auf x Achse? also x und y koordinate?
Um zu wissen, ob der Ball den Korb (Basket) trifft, muss man wissen wo der Korb ist. Aus der Aufgabe kann ich das nicht herauslesen. Vielleicht steht das in deinem Buch. Ansonsten kannst du nur den Landepunkt auf dem Boden bestimmen. Dort ist die Höhe 0m also f(x)=0. Das ist die rechte Nullstelle, die du bereits berechnet hast.
ok deine Erkärung verdeutlicht, aber warum erstmal die höhe y ist von der entferung abhängig? du meinst jetzt weil jede entfernug vom Werfer , eine unterschiedliche steigung hat ,und daruas folge auch unterschiedlcihe Höhe, aslo am anfagt steigt , bis der schietlpunkt
und dann geht wieder unten bis der ball den absket trifft.? richtig
eigentlich gibt mehr als 3 Punkte , ich habe nur 3 punkte geschrieben.
und noch wichtige Fragen, WARUM ist die y ( höhe) von der der Entfernug von vom Abwurfort, ABHÄNGIG
Aus der Physik weiß man, dass der Ball bei dem Experiment "schräger Wurf" ziemlich genau eine Parabelbahn beschreibt. also eine Funktion 2. Grades mit nach unten geöffneter Parabel. Wenn man 3 Punkte weiß, kann man daraus die Funktion bestimmen. Und dann ist für jede Entfernung x die Höhe f(x) eindeutig zu berechnen. Deshalb sagt man die Höhe ist abhängig von der Entfernung.
Wenn man eine Funktion hat, die auf der x-Achse die Zeit nach dem Start und auf der y-Achse den zurückgelegten Weg, dann sagt man "der Weg ist abhängig von der Zeit".
ich habe etwas geschrieben , hast du gesgehen?
ich gebe dir noch vierte Punktd
D(4,5 | 3,35)
Aber dieser 4. Punkt liegt nicht auf der Parabel, der Ball landet bei x=3,86. Wenn bei Punkt D der Korb sein soll, hat der Werfer viel zu kurz geworfen.
weiss du, ich denke die Aufgabe ist nicht in ordung, denn
schau mal bitte der Graph
im buch gibt er weitere Punkt, wenn ich diese Pnukt auf Graph sehe , stimmt das nicht
ich gebe dir mehere punkte damit du mir sage was die richtige gelcihung ist , und bitte sag mir ob ist meine Gleicnug die ich geschrieben habe überhaupt richtig ist
also die punkte sind
P( 0 | 2) B(0,5 | 2,75) c (1 |3,20) D (2 | 3,90 )D E (2,5 |4,05) F (3 | 4,10) G( 4,5 | 3,35)
Scheitelpunkt (1,5 | 3,35)
meine lösung lautet
f8x) = -0.6x^2+1,8x+2
nee , die Funktion im Buch nicht gegen, geneg nuir Punkt, aber die LÖsung seht im Lösungs buch , nicht in LehrBuch, also die Frage ist nur mit punkte, und ich muss gelcihung austellen.