Wie löst man eine trigonometrische Funktionsaufgabe?
Das Riesenrad hat einen Durchmesser von 120m. Der Einstieg liegt in 4 m Höhe über dem Erdboden. Das Rad rotiert stets um 460°, dann stoppt es kurz zum Ein- und Aussteigen.
1) In welcher Höhe befindet sich ein Fahrgast bei seinem fünften Zwischenstopp?
2) Nach welcher Zahl von Zwischenstopps kann man erstmals aussteigen
Ich komme bei der Aufgabe nicht weiter, mein Ansatz war folgend:
1) Berechnung des Umfang: U = d * π = 120m * π ~ 376,99m 5 Rotationen: 460° * 5 = 2300°
2300° / 376,99m = 6,10m
6 Antworten
2) 360° = 2 • 2 • 2 • 3 • 3 • 5 = 2³ • 3² • 5
460°- 360° = 100° = 2 • 2 • 5 • 5 = 2² • 5²
kleinstes gemeinsames Vielfache
2³ • 3² • 5² = 1800°
nach 1800°/100° = 18 Zwischenstopps
------------------------------------------
360° = 2 • 2 • 2 • 3 • 3 • 5 = 2³ • 3² • 5
460° = 2 • 2 • 5 • 23 = 2² • 5 • 23
kleinstes gemeinsames Vielfache
2³ • 3² • 5 • 23 = 8280°
8260° / 360° = 23 Umrundungen
Die Höhe des Einstiegs in Abhängigkeit des Drehwinkels a wird beschrieben durch
60 + sin(a) * 60
schwankt also zwischen 0 und 120 Metern.
Sieht man auf das Riesenrad und vergleicht es mit einer Uhr, legen wir den Winkel 0 auf 3 Uhr.
Für den Einstieg auf 4 Meter Höhe muss also gelten
60 + sin( we ) * 60 = 4, we = Winkel Einstieg
we = arcsin ( (4-60)/60 )
Dreht sich das Rad (im Uhrzeigersinn) 5 mal um 460 Grad, legt es 2300 Grad = (6 * 360 + 140 ) zurück, das Rad steht dann also am Winkel
we + 140.
Die Höhe ist dann also
60 + sin( we+140 ) * 60
Nach wievielen Zwischenstopps kann der Gast aussteigen ?
Dazu muss gelten 460 * a = 360 * b , a,b ganze Zahlen
460 * a = 360 * b
460 / 360 = b / a
Erster Ansatz
b = 460 a = 360
jetzt kürzen
b = 46 a = 36
b = 23 a = 18
Es sind also 18 Rotationen um 460 Grad. Dabei wird vorausgesetzt, dass man nur rechts ein- und aussteigen kann. Theoretisch wäre es ja auch auf der linken Seite möglich. Dazu wird in der Aufgabe aber nichts gesagt.
Etwas fehlt noch. In der Aufgabe wird nirgends gesagt, ob sich der Einstieg 4 Meter über dem tiefsten Punkt des Riesenrades befindet (Treppe / Rampe), oder aber am tiefsten Punkt. Im zweiten Fall ist die Rechnung noch einfacher.
zu a)
den Umfang benötigst du gar nicht!
beim 5. Zwischenstopp sind es 5*100° = 500°
500° -360° = 140°
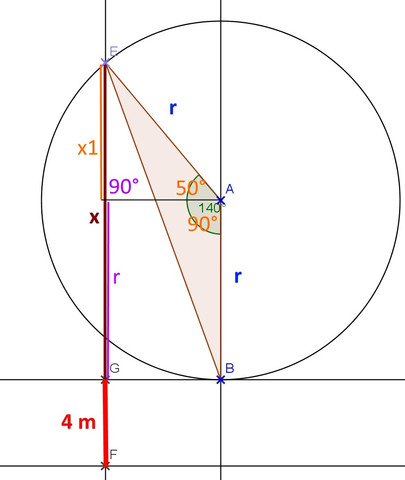
nun eine Skizze zeichnen:
Hoffe, du kommst mit dieser weiter!
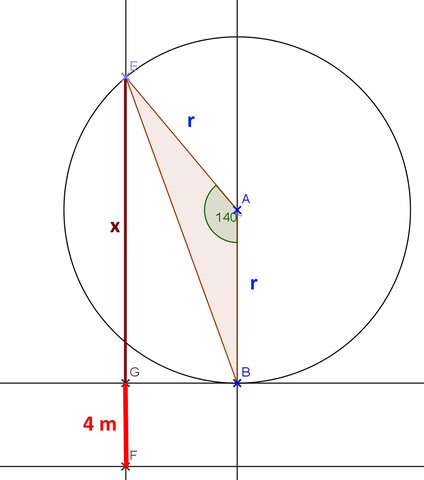
zu b)
360° ist eine Umdrehung.
Der Stopp ist bei 460° = 360° + 100°
Aussteigen kann man wieder, wenn ein Vielfaches von 360° mit den 100° erreicht wurde.
1800° = 5*360° = 18*100° => also nach 18 Stopps.
Skizze zu a) mit weiteren Hilfen