Mathe: Höhe eines Riesenrads mit trigonometrischen Funktionen?
Hallo,
man kann mit Hilfe von trigonometrischen Funktionen, also mit Sinus; Cosinus etc. die Höhe der Gondel eines Riesenrads in Abhängigkeit vom Winkel a berechnen.
Ich habe folgende Formel gefunden:
Höhe (a) = Radius * sin (a) + Höhe des Mittelpunkts (Aufhängung vom Riesenrad)
Wie genau soll das gehen?
Kann mir jemand die Gleichung erklären?
Danke für die Hilfe
4 Antworten
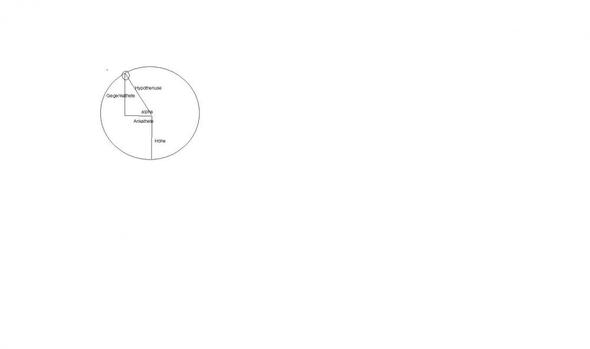
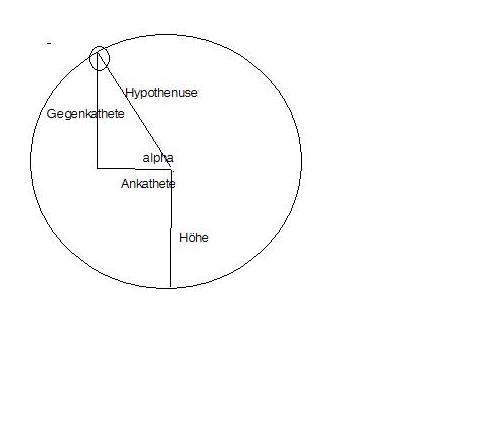
du kannst dir ein rechtwinkliges Dreieck an dein Riesenrad legen.
die Formel die du da hast war mal:
a=alpha
sin(a)=Gegenkathete/ Hypothenuse
das ganze nach Gegenkathete umgestellt ergibt;
sin(a)*Hypothenuse=Gegenkathete.
da das jetzt aber nur das Stück vom Mittelpunkt des Rades bis zur Gondel ist, musst du noch den Weg bis zum Mittelpunkt draufaddieren.
Gegenkathete=sin(a)*Hypothenuse+Höhe
ich hoffe es hilft dir weiter ;)
ein Kreis mit Radius r zeichnen; auf der Kreislininie im oberen Bereich eine Punkt A (Gondel) wählen; vom Mittelpunkt M des Kreises (Riesenrad) zwischen Waagerechter und MA liegt alpha=a ; dann sin a =x/r wobei x das kleine senkrechte Stück von A runter auf Waagerechte ist. dann umstellen x=r * sin a und um die ganze Höhe vom Boden zur Gondel zu erhalten dann +Höhe des Mittelpunktes.
besser
Danke für eure Antworten! Hab noch eine andere Frage: Mit welcher Funktionsgleichung kann man die Höhe der Gondel in Abhängigkeit der Zeit berechnen?