Wie löse ich diese Matheaufgabe?
Hallo , ich bräuchte Hilfe bei dieser Aufgabe... wir schreiben morgen Klassenarbeit und ich weiß nicht wie ich es lösen kann ...

2 Antworten
a) Nach 1 Jahr sind noch 5,5 g Schwefel vorhanden.
Nach 2 Jahren: 5,04 g
Nach 3 Jahren: 4,62 g
Nach 4 Jahren: 4,24 g
Nach 5 Jahren: 3,88 g
Nach 6 Jahren: 3,56 g
b) Die Funktionsgleichung lautet:
f(n)=m(11/12)^n
n=Anzahl der Jahre
m= 6 g
c) Nach 10 Jahren sind noch 2,51 g radioaktiver Schwefel vorhanden.
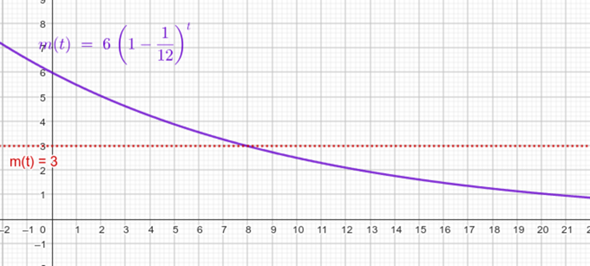
d) Die Halbwertszeit für den Schwefel in dieser Aufgabe beträgt ca. 8 Jahre.
Hinweis: Für Schwefel-35 beträgt die Halbwertszeit 87,51 Tage.
Aufgabe a)
nach 1 Jahr ist die Restmenge = 6 g - 6 g · 1/12 = 6 g - 1/2 g = 5,5 g
nach 2 Jahren ist die Restmenge = 5,5 g - 5,5 g · 1/12 = 5 - 0,45833 g = 5,04167 g
... und schon langweilig ..
Anders:
nach 1 Jahr ist die Restmenge = 6g - 6g · 1/12 = 6g·(1-1/12)=6g·(1-1/12)¹
nach 2 Jahren ist die Restmenge = 6g·(1-1/12) - 6g·(1-1/12)· 1/12 = 6g·(1-1/12)·(1-1/12) = 6g·(1-1/12)²
... hier zeichnet sich schon eher ab, wie die Funktionsgleichung lauten könnte:
Aufgabe b) Die Funktionsgleichung für die Restmenge lautet mit der Variablen t als die vergangene Zeit in Jahren und der Masse m in g:

Aufgabe c) Berechne m(10)
Aufgabe d) Halbwertszeit
Löse die Gleichung
Anmerkung: Ich habe kein Schwefel-Isotop mit dieser Halbwertszeit gefunden.