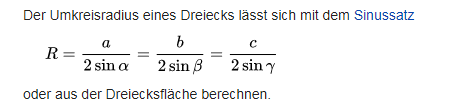Wie kann das gemacht werden?

Ein Designer hat dreieckige Spiegel entworfen : Eine Seite ist 14 cm lang , die beiden anliegenden Winkel sind 60 ° und 50 ° groß . Diese Spiegelfläche soll auf einer kreisförmigen Holz scheibe befestigt werden . Bestimme deren Durchmesser .

Answer 1

[mihisu]

Wenn man ein Dreieck hat mit einem Innenwinkel α gegenüber einer Seite mit Länge a, so erhält man für den Durchmesser d des Umkreises:

$d=\frac{a}{\sin\left(\alpha\right)}$

[Das kann man mit Peripheriewinkelsatz und Sinussatz zeigen.]

Im konkreten Fall erhält man für den Innenwinkel gegenüber der 14 cm langen Seite aufgrund der Innenwinkelsumme 180° - 60° - 50° = 70°.

Für den gesuchten Durchmesser erhält man demnach im konkreten Fall:

$d=\frac{14\ \text{cm}}{\sin\left(70\degree\right)}\approx14,90\ \text{cm}\$

Comments

[Halbrecht]

ja , ich hatte noch überlegt , das die beiden gegebenen Winkel ja nicht eindeutig sind, aber Gamma ist es.

Answer 2

[gauss58]

Hinweise:

Der Schnittpunkt der Mittelsenkrechten ist der Mittelpunkt des Umkreises.

Den Radius des Umkreises kann man aus einer Seite und dem Sinus des gegenüberliegenden Winkels berechnen.

Answer 3

[Halbrecht]

man braucht den radius des Umkreises

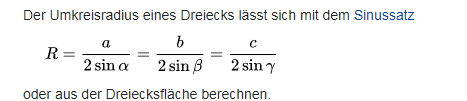
a = 14 cm

Wenn man beta als 60 Grad bestimmt , also der Winkel den man am Anfang der 14cm konstruiert an der Seite a beim Punkt B , gilt eben R = a / 2sin(60) , sonst R= a/2sin(50)

einfacher und vor alles eindeutiger sollte es gehen , wenn man die 14 als c betrachtet ! C gegenüber liegt gamma und mit

R = c / 2*sin(180-60-50) ist man sofort am Ziel.