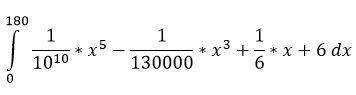Weiß jemand, wie ich diese Matheaufgabe rechnen kann?
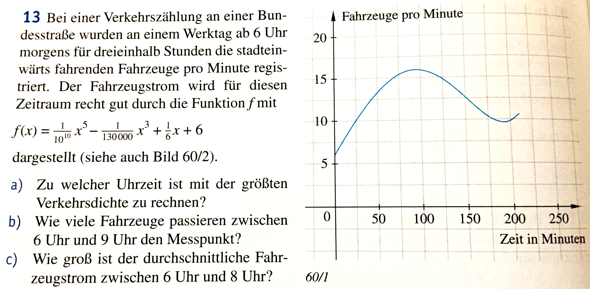
Kann jemand die Matheaufgabe rechnen? Komme bei der Integralrechnung nicht mehr hinterher
4 Antworten
bei Der c musst du einfach das integral von 0 bis 120 bestimmen und dann geteilt durch 120
also Stammfunktion dann (F(120 ) - F(0) ) /120
f(x)=1/(10¹⁰)*x⁵-1/130000*x³+1/6*x+6 abgeleitet
f´(x)=m=0=4/(10¹⁰)*x⁴-3/130000*x²+1/6
Mit meinem Graphikrechner (GTR,Casio) x=85,667
Probe: f´(85,667)=4/(10¹⁰)*85,667⁴-3/130000*85,667²+1/6=-5,36*10^(-4)=0 bis auf Rundungsfehler
noch mal abgeleitet,um zu prüfen,ob ein Maximum oder Minimum vorliegt.
f´´(x)=20/(10¹⁰)*x³-6/130000*x
f´´(85,667)=20/(10¹⁰)*85,667³-6/130000*85,667=-3,828..<0 also ein Maximum
f(x)=.... integriert
F(x)=Integral((1/(10¹⁰)*x⁵-1/130000*x³+1/6*x+6)*dx
F(x)=1/(10¹⁰)*Int.(x⁵*dx)-1/130000*Int.(x³*dx)+1/6*Int.(x*dx)+6*Int.(dx)
=1/(10¹⁰)*x^(5+1)*1/(5+1)-1/130000*x^(3+1)*1/(3+1)+1/6*x^(1+1)*1/(1+1)+6*x+C
=1/(10¹⁰)*x⁶*1/6-1/130000*x⁴*1/4+1/6*x²*1/2+6*x+C
F(x)=1/(6*10¹⁰)*x⁶-1/520000*x⁴+1/12*x²+6*x+C
A=obere Grenze minus untere Grenze xu=0 Minuten xo=180 Minuten
Die Integrationskonstante C hebt sich dabei auf
Anzahl der Fahrzeuge=(F(xo)) - (F(xu))
Anzahl der Fahrzeuge =(F(180)) - (F(0))=....
c)
Differenzenquotient m=(y2-y1)/(x2-x1)
durchschnittliche Anzahl der Fahrzeuge je Minute=f(t2) - f(t1)/(t2-t1)
t1=0 Minuten bei 6 Minuten y1=6 Fahrzeuge pro Minute
t2=120 Minuten von 6 Uhr bis 8 Uhr sind 2 Stunden ,also t2=2*60 min=120 min
f(t1)=f(0)=...=6
f(t2)=f(120)=.....= selber ausrechnen
Den Rest schaffst du selber.
Hinweis: Der Funktionswert stimmt bei f(200)=..... so mit dem Diagramm nicht überein.
Hallo lena1234554,
bei a) ist der Hochpunkt gesucht. Diesen bestimmst du mit der 1. Ableitung. Diese setzt du = 0.
Ich habe eine Lösung von x = 94,6 (kommt ja hin wenn du dir die Grafik anschaust) (bzw t wir reden ja von Zeit)
Also 6:00 Uhr + 94 Min ist 7:34 Uhr.
b) bis 9:00 Uhr. Also 3 h lang...
Du brauchst also das Integral von f(x) und setzt die Integralgrenzen auf 0 min und 180 min
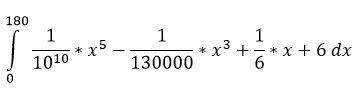
Das kannst du easy integrieren, da es einzelne Summanden sind ^^
ich habe 2328 Fahrzeuge raus