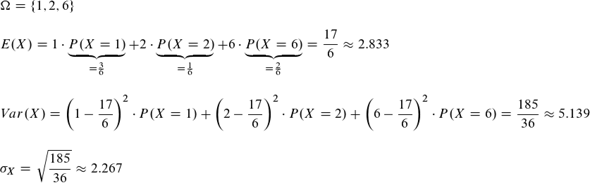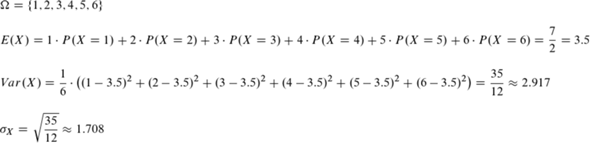Wahrscheinlichkeiten Mathe?
Hallo!
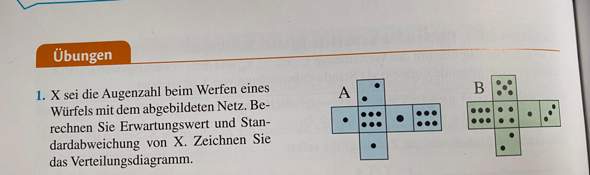
Ich bräuchte Hilfe bei dieser Aufgabe. Ich weiß, wie ich alles berechnen muss, doch wie soll ich den Erwartungswert berechne, wenn ich nicht weiß, was xi ist (ist xi 1,2,3,4,5,6?). Wieso sind da zwei abgebildete Netze?
Ich habe für den Erwartungswert = 3,1667
und für die Standardabweichung 2,0333
Ist das richtig?
2 Antworten
das sind 2 Aufgabenteile A und B
x_i ist die Augenzahl
bei A gibts nur 1, 2 und 6
bei B 1, 2, ... 6
bei A ist
Erwartungswert E(X) = 1*1/2 + 2*1/6 + 6*1/3 = 2.833
Varianz Var(X)=(1-2.833)²*1/2 + (2-2.833)²*1/6 + (6-2.833)²*1/3 = 5.139
Standardabweichung sigma = Wurzel(Var(X)) = 2.267
Und die Standardabweichung bei A ist die Wurzel {[2*(6-E)²+(2-E)²+3*(1-E)²]/6}.
Das ist die Abweichung, die mit dem kleinen griechischen sigma bezeichnet wird.
Die Abweichung, deren Symbol ein kleines s ist, und die die Erwartungstreue berücksichtigt, bekommst Du, wenn Du den Zähler unter der Wurzel nicht durch n=6, sondern durch n-1=5 teilst.
Würfel A
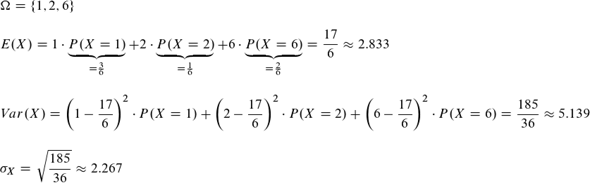
Würfel B
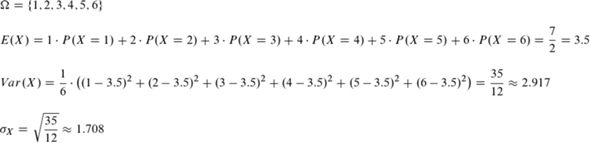
Man darf bei Würfel B nicht vergessen, dass es eine gleich verteilte Wahrscheinlichkeitsverteilung bzw. ein Laplace-Experiment ist - man kann also ⅙ ausklammern.
Ich hoffe, ich konnte helfen :)